【题目】如图,排球运动员站在点O处练习发球,将球从点O正上方2米的点A处发出把球看成点,其运行的高度y(米)与运行的水平距离x(米)满足关系式y=a(x﹣6)2+h,已知球网与点O的水平距离为9米,高度为2.43米,球场的边界距点O的水平距离为18米.
(1)当h=2.6时,求y与x的函数关系式.
(2)当h=2.6时,球能否越过球网?球会不会出界?请说明理由.
(3)若球一定能越过球网,又不出边界.则h的取值范围是多少?

参考答案:
【答案】(1)y=﹣![]() (x﹣6)2+2.6,(2)会出界;(3)h的取值范围是:h≥
(x﹣6)2+2.6,(2)会出界;(3)h的取值范围是:h≥![]() .
.
【解析】试题分析:(1)利用h=2.6将点(0,2),代入解析式求出即可;
(2)利用当x=9时,y=﹣![]() (x﹣6)2+2.6=2.45,当y=0时,
(x﹣6)2+2.6=2.45,当y=0时, ![]() ,分别得出即可;
,分别得出即可;
(3)根据当球正好过点(18,0)时,抛物线y=a(x﹣6)2+h还过点(0,2),以及当球刚能过网,此时函数解析式过(9,2.43),抛物线y=a(x﹣6)2+h还过点(0,2)时分别得出h的取值范围,即可得出答案.
试题解析:解:(1)∵h=2.6,球从O点正上方2m的A处发出,
∴抛物线y=a(x﹣6)2+h过点(0,2),
∴2=a(0﹣6)2+2.6,
解得:a=﹣![]() ,
,
故y与x的关系式为:y=﹣![]() (x﹣6)2+2.6,
(x﹣6)2+2.6,
(2)当x=9时,y=﹣![]() (x﹣6)2+2.6=2.45>2.43,
(x﹣6)2+2.6=2.45>2.43,
所以球能过球网;
当y=0时, ![]() ,
,
解得:x1=6+2![]() >18,x2=6﹣2
>18,x2=6﹣2![]() (舍去)
(舍去)
故会出界;
(3)当球正好过点(18,0)时,抛物线y=a(x﹣6)2+h还过点(0,2),代入解析式得:
![]() ,
,
解得:  ,
,
此时二次函数解析式为:y=﹣![]() (x﹣6)2+
(x﹣6)2+![]() ,
,
此时球若不出边界h≥![]() ,
,
当球刚能过网,此时函数解析式过(9,2.43),抛物线y=a(x﹣6)2+h还过点(0,2),代入解析式得:
![]() ,
,
解得:  ,
,
此时球要过网h≥![]() ,
,
故若球一定能越过球网,又不出边界,h的取值范围是:h≥![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】智能手环是一种穿戴式智能设备,通过智能手环,用户可以记录日常生活中的锻炼,睡眠、部分还有饮食等实时数据,并将这些数据与手机、平板同步,起到通过数据指导健康生活的作用,某公司2020年3月新推出
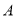 型和
型和 型两款手环.
型两款手环.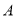 型手环每只售价是
型手环每只售价是 型手环售价的1.5倍.3月份
型手环售价的1.5倍.3月份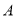 、
、 手环总计销售650只,
手环总计销售650只,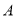 型手环销售额为108000元,
型手环销售额为108000元, 型手环销售额为84000元.
型手环销售额为84000元.(1)求
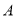 、
、 型手环的售价各是多少?
型手环的售价各是多少?(2)由于更多的公司研发手环投入市场,市场竞争的加剧,公司决定4月份对两种手环进行降价促销,对
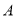 型手环直降
型手环直降 元,销量比原来提高了
元,销量比原来提高了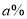 ,对
,对 型手环在原价基础上降价
型手环在原价基础上降价 销售,销量比原来提高了20%,4月份总计销售额为208320元,求
销售,销量比原来提高了20%,4月份总计销售额为208320元,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某数学兴趣小组在全校范围内随机抽取了50名同学进行“舌尖上的长沙﹣我最喜爱的长沙小吃”调查活动,将调查问卷整理后绘制成如图所示的不完整条形统计图:

请根据所给信息解答以下问题:
(1)请补全条形统计图;
(2)若全校有2000名同学,请估计全校同学中最喜爱“臭豆腐”的同学有多少人?
(3)在一个不透明的口袋中有四个完全相同的小球,把它们分别标号为四种小吃的序号A、B、C、D,随机地摸出一个小球然后放回,再随机地摸出一个小球,请用列表或画树形图的方法,求出恰好两次都摸到“A”的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某服装厂生产一种西装和领带,西装每套定价
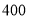 元,领带每条定价
元,领带每条定价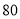 元,厂方在开展促销活动期间,向客户提供两种优惠方案:
元,厂方在开展促销活动期间,向客户提供两种优惠方案:①买一套西装送一条领带;
②西装和领带都按定价的
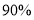 付款.
付款.现某客户要到该服装厂购买西装
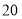 套,领带
套,领带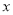 条(
条( ).
).(1)客户分别按方案①、方案②购买,各需付款多少元?(用含
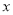 的代数式表示);
的代数式表示);(2)若
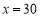 ,通过计算说明此时按哪种方案购买较为合算?
,通过计算说明此时按哪种方案购买较为合算? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC在正方形网格中,若A(0,3),按要求回答下列问题
(1)在图中建立正确的平面直角坐标系;
(2)根据所建立的坐标系,写出B和C的坐标;
(3)计算△ABC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】两块等腰直角三角形纸片AOB和COD按图1所示放置,直角顶点重合在点O处,AB=25,CD=17.保持纸片AOB不动,将纸片COD绕点O逆时针旋转α(0°<α<90°)角度,如图2所示.
(1)利用图2证明AC=BD且AC⊥BD;
(2)当BD与CD在同一直线上(如图3)时,求AC的长和α的正弦值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:
材料1:对于一个关于
 的二次三项式
的二次三项式
 ,除了可以利用配方法求请多项式的取值范围外,爱思考的小川同学还想到了其他的方法:比如先令
,除了可以利用配方法求请多项式的取值范围外,爱思考的小川同学还想到了其他的方法:比如先令
 ,然后移项可得:
,然后移项可得: ,再利用一元二次方程根的判别式来确定
,再利用一元二次方程根的判别式来确定 的取值范围,请仔细阅读下面的例子:
的取值范围,请仔细阅读下面的例子:例:求
 的取值范围:
的取值范围:解:令

∴

∴

∴

∴
 ;
;材料2:在学习完一元二次方程的解法后,爱思考的小川同学又想到仿造一元二次方程的解法来解决一元二次不等式的解集问题,他的具体做法如下:
若关于
 的一元二次方程
的一元二次方程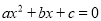 (
( )有两个不相等的实数根
)有两个不相等的实数根 ,
, (
( )
)则关于
 的一元二次不等式
的一元二次不等式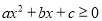 (
( )的解集为:
)的解集为: 或
或 .
.则关于
 的一元二次不等式
的一元二次不等式 (
( )的解集为:
)的解集为: .
.请根据上述材料,解答下列问题:
(1)若关于
 的二次三项式
的二次三项式 (
( 为常数)的最小值为-6,则
为常数)的最小值为-6,则 ________;
________;(2)求出代数式
 的取值范围;
的取值范围;(3)若关于
 的代数式
的代数式 (其中
(其中 、
、 为常数,且
为常数,且 )的最小值为-4,最大值为7,请求出满足条件的
)的最小值为-4,最大值为7,请求出满足条件的 ,
, 的值.
的值.
相关试题

