【题目】若两条抛物线的顶点相同,则称它们为“友好抛物线”,抛物线![]() :
:![]() 与
与![]() :
:![]() 为“友好抛物线”.
为“友好抛物线”.
(1)求抛物线![]() 的解析式.
的解析式.
(2)点A是抛物线![]() 上在第一象限的动点,过A作AQ⊥x轴,Q为垂足,求AQ+OQ的最大值.
上在第一象限的动点,过A作AQ⊥x轴,Q为垂足,求AQ+OQ的最大值.
(3)设抛物线![]() 的顶点为C,点B的坐标为(﹣1,4),问在
的顶点为C,点B的坐标为(﹣1,4),问在![]() 的对称轴上是否存在点M,使线段MB绕点M逆时针旋转90°得到线段MB′,且点B′恰好落在抛物线
的对称轴上是否存在点M,使线段MB绕点M逆时针旋转90°得到线段MB′,且点B′恰好落在抛物线![]() 上?若存在求出点M的坐标,不存在说明理由.
上?若存在求出点M的坐标,不存在说明理由.
参考答案:
【答案】(1) ![]() ;(2) 当a=
;(2) 当a=![]() 时,AQ+OQ有最大值,最大值为
时,AQ+OQ有最大值,最大值为![]() (3)存在点M,(1,2)或(1,5).
(3)存在点M,(1,2)或(1,5).
【解析】
试题分析:(1)先求得![]() 顶点坐标,然后依据两个抛物线的顶点坐标相同可求得m、n的值;
顶点坐标,然后依据两个抛物线的顶点坐标相同可求得m、n的值;
(2)设A(a,![]() ).则OQ=x,AQ=
).则OQ=x,AQ=![]() ,然后得到OQ+AQ与a的函数关系式,最后依据配方法可求得OQ+AQ的最值;
,然后得到OQ+AQ与a的函数关系式,最后依据配方法可求得OQ+AQ的最值;
(3)连接BC,过点B′作B′D⊥CM,垂足为D.接下来证明△BCM≌△MDB′,由全等三角形的性质得到BC=MD,CM=B′D,设点M的坐标为(1,a).则用含a的式子可表示出点B′的坐标,将点B′的坐标代入抛物线的解析式可求得a的值,从而得到点M的坐标.
试题解析:(1)∵![]() =
=![]() ,
,
∴抛物线![]() 的顶点坐标为(1,4).
的顶点坐标为(1,4).
∵抛物线![]() 与
与![]() 顶点相同,
顶点相同,
∴![]() =1,﹣1+m+n=4.
=1,﹣1+m+n=4.
解得:m=2,n=3.
∴抛物线![]() 的解析式为
的解析式为![]() ;
;
(2)如图1所示:

设点A的坐标为(a,![]() ).
).
∵AQ=![]() ,OQ=a,
,OQ=a,
∴AQ+OQ=![]() +a=
+a=![]() =
=![]() .
.
∴当a=![]() 时,AQ+OQ有最大值,最大值为
时,AQ+OQ有最大值,最大值为![]() .
.
(3)存在点M,理由如下:
如图2所示;连接BC,过点B′作B′D⊥CM,垂足为D.

∵B(﹣1,4),C(1,4),抛物线的对称轴为x=1,
∴BC⊥CM,BC=2.
∵∠BMB′=90°,
∴∠BMC+∠B′MD=90°.
∵B′D⊥MC,
∴∠MB′D+∠B′MD=90°.
∴∠MB′D=∠BMC.
在△BCM和△MDB′中,∠MB′D=∠BMC ,∠BCM=∠MDB′,BM=MB′,
∴△BCM≌△MDB′.
∴BC=MD,CM=B′D.
设点M的坐标为(1,a).则B′D=CM=4﹣a,MD=CB=2.
∴点B′的坐标为(a﹣3,a﹣2).
∴![]() ,
,
整理得:![]() ﹣7a+10=0.
﹣7a+10=0.
解得a=2,或a=5.
当a=2时,M的坐标为(1,2),
当a=5时,M的坐标为(1,5).
综上所述当点M的坐标为(1,2)或(1,5)时,B′恰好落在抛物线![]() 上.
上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图一根木棒放在数轴上,数轴的1个单位长度为1cm,木棒的左端与数轴上的点A重合,右端与点B重合.

(1)若将木棒沿数轴向右水平移动,则当它的左端移动到点B时,它的右端在数轴上所对应的数为20;若将木棒沿数轴向左水平移动,则当它的右端移动到A点时,则它的左端在数轴上所对应的数为5,由此可得到木棒长为cm.
(2)图中点A所表示的数是 , 点B所表示的数是 .
(3)由题(1)(2)的启发,请你能借助“数轴”这个工具帮助小红解决下列问题:
一天,小红去问曾当过数学老师现在退休在家的爷爷的年龄,爷爷说:“我若是你现在这么大,你还要40年才出生;你若是我现在这么大,我已经125岁,是老寿星了,哈哈!”,请求出爷爷现在的年龄 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知﹣xmy2+3n与5x2n﹣3y8的和是单项式,则m、n的值分别是( )
A.m=2,n=1
B.m=1,n=1
C.m=1,n=3
D.m=1,n=2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,用火柴杆摆出一系列三角形图案,共摆有n层,当n=1时,需3火柴;当n=2时,需9根火柴,按这种方式摆下去,
(1)当n=3时,需 根火柴.
(2)当n=20时,需 根火柴.
(3)用含n的式子写出规律来______________________________
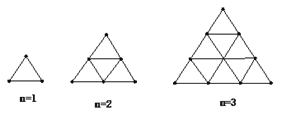
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一个两位数的个位数字与十位数字相互交换位置,得到另一个两位数,则这个新两位数与原来两位数的差,一定可以被( )
A.2整除
B.3整除
C.6整除
D.11整除 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点M(3,﹣2),将它先向左平移2个单位,再向上平移4个单位后得到点N,则点N的坐标是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式2a3﹣18a=_____.
相关试题

