搜索
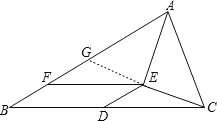
【题目】如图，在△ABC中，点D为边BC的中点，点E在△ABC内，AE平分∠BAC，CE⊥AE点F在AB上，且BF=DE
（1）求证：四边形BDEF是平行四边形
（2）线段AB，BF，AC之间具有怎样的数量关系？证明你所得到的结论
参考答案：
【答案】（1）见解析；（2）
，理由见解析
【解析】
（1）延长CE交AB于点G，证明
，得E为中点，通过中位线证明DE
AB，结合BF=DE，证明BDEF是平行四边形
（2）通过BDEF为平行四边形，证得BF=DE=
BG，再根据，得AC=AG，用AB-AG=BG，可证
（1）证明：延长CE交AB于点G
∵AE
CE
∴
在和
∴
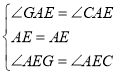
∴GE=EC
∵BD=CD
∴DE为
的中位线
∴DEAB
∵DE=BF
∴四边形BDEF是平行四边形
（2）
理由如下：
∵四边形BDEF是平行四边形
∴BF=DE
∵D，E分别是BC，GC的中点
∴BF=DE=BG
∵
∴AG=AC
BF=（AB-AG）=（AB-AC）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，每个小正方形的边长为1cm
（1）求四边形ABCD的面积；
（2）四边形ABCD中有直角吗？若有，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】网店店主小李进了一批某种商品，每件进价10元.预售一段时间后发现：每天销售量
（件）与售价
（元/件）之间成一次函数关系：
.（1）小李想每天赚取利润150元，又要使所进的货尽快脱手，则售价定为多少合适？
（2）小李想每天赚取利润300元，这个想法能实现吗？为什么？
-
科目： 来源： 题型：
查看答案和解析>>【题目】一辆客车从甲地开往乙地，一辆出租车从乙地开往甲地，两车同时出发，设客车离甲地的距离为
千米，出租车离甲地的距离为
千米，两车行驶的时间为x小时，、关于x的图象如图所示：
（1）根据图象，分别写出
、关于x的关系式（需要写出自变量取值范围）；（2）当两车相遇时，求x的值；
（3）甲、乙两地间有
、
两个加油站，相距200千米，若客车进入加油站时，出租车恰好进入加油站，求加油站离甲地的距离． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知直线
，点
、
在直线
上，点
、
在直线
上，点在点的右侧，
，
，
平分
，
平分
，直线、交于点
．
（1）写出
的度数 ；（2）试求
的度数（用含n的代数式表示）；（3）将线段
向右平行移动，使点在点的右侧，其他条件不变，请画出图形并直接写出的度数（用含n的代数式表示）． -
科目： 来源： 题型：
查看答案和解析>>【题目】计算
（1）
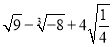
（2）[－4a2b2＋ab（20a2－ab）]÷（－2a2）；
（3）（x＋3）（x＋4）－（x－1）2；
（4）
-
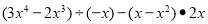
科目： 来源： 题型：
查看答案和解析>>【题目】（1）解不等式2（4x-1）≥5x-8，并把它的解集在数轴上表示出来．
（2）如图，在平面直角坐标系xOy中，△ABC的三个顶点的坐标分别是A（-3，0），B（-6，-2）C（-2，-5）．将△ABC向上平移3个单位长度，再向右平移5个单位长度，得到△A1B1C1．
①在平面直角坐标系xOy中画出△A1B1C1．
②求△A1B1C1的面积．
相关试题
