【题目】点O为直线AB上一点,过点O作射线OC,使∠BOC=65°,将一直角三角板的直角顶点放在点O处.
(1)如图①,将三角板MON的一边ON与射线OB重合时,则∠MOC= ;
(2)如图②,将三角板MON绕点O逆时针旋转一定角度,此时OC是∠MOB的角平分线,求旋转角∠BON和∠CON的度数;
(3)将三角板MON绕点O逆时针旋转至图③时,∠NOC=![]() ∠AOM,求∠NOB的度数.
∠AOM,求∠NOB的度数.

参考答案:
【答案】(1)25°;(2)25°;(3)70°.
【解析】
试题分析:(1)根据∠MON和∠BOC的度数可以得到∠MON的度数.
(2)根据OC是∠MOB的角平分线,∠BOC=65°可以求得∠BOM的度数,由∠NOM=90°,可得∠BON的度数,从而可得∠CON的度数.
(3)由∠BOC=65°,∠NOM=90°,∠NOC=![]() ∠AOM,从而可得∠NOC的度数,由∠BOC=65°,从而得到∠NOB的度数.
∠AOM,从而可得∠NOC的度数,由∠BOC=65°,从而得到∠NOB的度数.
解:(1)∵∠MON=90°,∠BOC=65°,
∴∠MOC=∠MON﹣∠BOC=90°﹣65°=25°.
故答案为:25°.
(2)∵∠BOC=65°,OC是∠MOB的角平分线,
∴∠MOB=2∠BOC=130°.
∴∠BON=∠MOB﹣∠MON
=130°﹣90°
=40°.
∠CON=∠COB﹣∠BON
=65°﹣40°
=25°.
(3)∵∠NOC![]() ∠AOM,
∠AOM,
∴∠AOM=4∠NOC.
∵∠BOC=65°,
∴∠AOC=∠AOB﹣∠BOC
=180°﹣65°
=115°.
∵∠MON=90°,
∴∠AOM+∠NOC=∠AOC﹣∠MON
=115°﹣90°
=25°.
∴4∠NOC+∠NOC=25°.
∴∠NOC=5°.
∴∠NOB=∠NOC+∠BOC=70°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一件服装标价200元,若以六折销售,仍可获利20℅,则这件服装进价是
A.100元 B.105元 C.108元 D.118元
-
科目: 来源: 题型:
查看答案和解析>>【题目】请你写出一个含有字母a、b且系数为﹣1,次数为3的单项式_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,真命题是( )
A.邻边之比相等的两个平行四边形一定相似B.邻边之比相等的两个矩形一定相似
C.对角线之比相等的两个平行四边形一定相似D.对角线之比相等的两个矩形一定相似
-
科目: 来源: 题型:
查看答案和解析>>【题目】解答题。
(1)先化简,再求值:(a+2)2﹣(a+1)(a﹣1),其中a=﹣ .
.
(2)已知m﹣n=﹣4,mn=2,求下列代数式的值.
①m2+n2
②(m+1)(n﹣1) -
科目: 来源: 题型:
查看答案和解析>>【题目】下面是小明做的一道题目以及他的解题过程:

题目:在同一平面上,若∠BOA=75°,∠BOC=22°,求∠AOC的度数,
解:根据题意可画图,如图所示,AOC=∠BOA-∠BOC=75°-22°=53°.
如果你是老师,能判小明满分吗?若能,请说明理由,若不能,请将错误指出来,并给出你认为正确的解法.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一块长为a米、宽为b米的长方形空地,现计划在这块空地中间修出两条互相垂直的宽均为2米的道路(图中阴影部分),其余部分进行绿化.
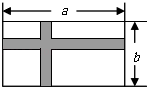
(1)求出绿地的面积;(用含a、b的代数式表示)
(2)若a=2b,且道路的面积为116米2 , 求原长方形空地的宽.
相关试题

