【题目】如图,在![]() 中,
中,![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() .动点
.动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向以
方向以![]() 的速度向点
的速度向点![]() 运动;同时动点
运动;同时动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向以
方向以![]() 的速度向点
的速度向点![]() 运动,运动时间是
运动,运动时间是![]() 秒.
秒.

(1)用含![]() 的代数式表示
的代数式表示![]() 的长度.
的长度.
(2)在运动过程中,是否存在某一时刻![]() ,使点
,使点![]() 位于线段
位于线段![]() 的垂直平分线上?若存在,求出
的垂直平分线上?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(3)是否存在某一时刻![]() ,使
,使![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(4)是否存在某一时刻![]() ,使
,使![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
参考答案:
【答案】(1)CP=8-3t;(2)见解析;(3)见解析;(4)见解析.
【解析】
(1)直接利用![]() 即可求解;
即可求解;
(2)根据线段垂直平分线的性质可得![]() ,列方程求解即可;
,列方程求解即可;
(3)根据全等三角形的性质可得若![]() ,因为
,因为![]() ,
,![]() ,
,
所以只需![]() ,列方程求出
,列方程求出![]() 的值即可;
的值即可;
(4)若![]() ,因为
,因为![]() ,所以需满足
,所以需满足![]() 且
且![]() ,即
,即![]() 且
且![]() ,没有符合条件的t的值,故不存在.
,没有符合条件的t的值,故不存在.
解:(1)![]() ;
;
(2)若点![]() 位于线段
位于线段![]() 的垂直平分线上,
的垂直平分线上,
则![]() ,
,
即![]() ,
,
解得![]() .
.
所以存在,![]() 秒时点
秒时点![]() 位于线段
位于线段![]() 的垂直平分线上.
的垂直平分线上.
(3)若![]() ,
,
因为![]() ,
,![]() ,
,
所以只需![]() ,
,
即![]() ,解得
,解得![]() ,
,
所以存在![]() .
.
(4)若![]() ,
,
因为![]() ,
,
所以需满足![]() 且
且![]() ,
,
即![]() 且
且![]() ,
,
所以![]() 不存在.
不存在.
故答案为:(1)CP=8-3t;(2)见解析;(3)见解析;(4)见解析.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线
 经过点
经过点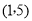 和
和 ,分别与x轴、y轴交于A、B两点.
,分别与x轴、y轴交于A、B两点.(1)求直线
 的解析式:
的解析式:(2)若把横、纵坐标均为整数的点称为格点,则图中阴影部分(不包括边界)所含格点的个数有 个;
(3)作出点
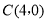 关于直线
关于直线 的对称点
的对称点 ,则点
,则点 的坐标为 ;
的坐标为 ;
(4)若在直线
 和
和 轴上分别存在一点
轴上分别存在一点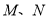 使
使 的周长最短,请在图中标出点
的周长最短,请在图中标出点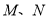 (不写作法,保留痕迹).
(不写作法,保留痕迹).
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明、小军两同学做游戏,游戏规则是:一个不透明的文具袋中,装有型号完全相同的3个红球和2个黑球,两人先后从袋中取出一个球(不放回),若两人所取球的颜色相同,则小明胜;否则,小军胜;
(1)请用树状图法求出摸笔游戏所有可能的结果;
(2)计算小明获胜的概率是 ,小军获胜的概率是 ,并指出本游戏规则是否公平,若不公平,你认为对谁有利.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=4,AD=5,AD、AB、BC分别与⊙O相切于E、F、G三点,过点D作⊙O的切线交BC于点M,则DM的长为( )

A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】春节前小明花1200元从市场购进批发价分别为每箱30元与50元的
 、
、 两种水果进行销售,分别以每箱35元与60元的价格出售,设购进
两种水果进行销售,分别以每箱35元与60元的价格出售,设购进 水果
水果 箱,
箱, 水果
水果 箱.
箱.(1)求
 关于
关于 的函数表达式;
的函数表达式;(2)若要求购进
 水果的数量不少于
水果的数量不少于 水果的数量,则应该如何分配购进
水果的数量,则应该如何分配购进 、
、 水果的数量并全部售出才能获得最大利润,此时最大利润是多少?
水果的数量并全部售出才能获得最大利润,此时最大利润是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】为了尽快实施“脱贫致富奔小康”宏伟意图,某县扶贫工作队为朝阳沟村购买了一批苹果树苗和梨树苗,已知一棵苹果树苗比一棵梨树苗贵2元,购买苹果树苗的费用和购买梨树苗的费用分别是3500元和2500元.
(1)若两种树苗购买的棵数一样多,求梨树苗的单价;
(2)若两种树苗共购买1100棵,且购买两种树苗的总费用不超过6000元,根据(1)中两种树苗的单价,求梨树苗至少购买多少棵.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若规定两数a、b通过“※”运算,得到4ab,即a※b=4ab,例如2※6=4×2×6=48
(1)求3※5的值;
(2)求x※x+2※x-2※4=0中x的值;
(3)若无论x是什么数,总有a※x=x,求a的值.
相关试题

