【题目】小明和小亮相约晨练跑步,小明比小亮早1分钟离开家门,3分钟后迎面遇到从家跑来的小亮,两人沿滨江路跑了2分钟后,决定进行长跑比赛,比赛时小明的速度始终是180米/分,小亮的速度始终是220米/分.如图是两人之间的距离y(米)与小明离开家的时间x(分)之间的函数图象,则下列结论中正确的是____________________.(写序号即可)
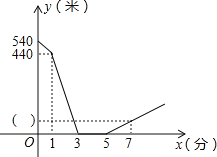
①小明家与小亮家距离为540米;
②小亮比赛前的速度为120米/分;
③小明出发7分钟时,两人距离为80米;
④若小亮从家出门跑了14分钟后,按原路以比赛时的速度返回,则再经过1分钟两人相遇.
参考答案:
【答案】①②③④
【解析】
根据函数图象可以求出小明比赛前的速度为(540-440)÷1=100米/分,甲乙两家的距离为540米,根据速度×时间=路程就可以求出小亮在比赛前的速度与220比较久可以确定是否发生变化,根据比赛时甲乙的速度关系就可以求出比赛2分钟时甲乙的距离,先求出14分钟时小亮在小明前面的距离,再由相遇问题就可以求出结论.
由函数图象及题意,得
①小明与小亮家相距:540米;故①正确;
②小亮比赛前的速度,由2×(v1+v2)=440,得v2=120m/min;故②正确;
③小明离家7分钟时两人之间的距离为:(7-5)(220-180)=80米;故③正确;
④小亮从家出门跑了14分钟后两人之间的距离为:(15-5)(220-180)=400米,
小亮返回时与小明相遇的时间为:400÷(180+220)=1分钟,故④正确;
∴正确的有①②③④.
故答案为:①②③④.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商品现在售价为每件60元,每星期可卖出300件,市场调查反映:调整价格,每件涨价1元,每星期要少卖出10件;每件降价1元,每星期可多卖出20件.已知商品的进价为每件40元.
(1)设每件降价x元,每星期的销售利润为y元;
① 请写出y与x之间的函数关系式;
② 确定x的值,使利润最大,并求出最大利润;
(2)若涨价x元,则x= 元时,利润y的最大值为 元(直接写出答案,不必写过程).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程
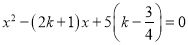 .
.(1)求证:无论k取何值,该方程总有实数根;
(2)若等腰
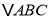 的一边长
的一边长 ,另两边b、c恰好是该方程的两个根,求
,另两边b、c恰好是该方程的两个根,求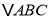 的周长.
的周长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,对角线AC,BD相交于点O,AO=CO,BO=DO,且∠ABC+∠ADC=180°.

(1)求证:四边形ABCD是矩形;
(2)若∠ADF:∠FDC=3:2,DF⊥AC,求∠BDF的度数.
-
科目: 来源: 题型:
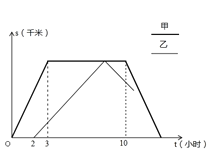
查看答案和解析>>【题目】甲乙两车从A市去往B市,甲比乙出发了2个小时,甲到达B市后停留一段时间返回,乙到达B市后立即返回.甲车往返的速度都为40千米/时,乙车往返的速度都为20千米/时,下图是两车距A市的路程S(千米)与行驶时间t(小时)之间的函数图象,请结合图象回答下列问题:
(1)A、B两市的距离是 千米,甲到B市后 小时乙到达B市;
(2)求甲车返回时的路程s(千米)与时间t(小时)之间的函数关系式,并写出自变量t的取值范围;
(3)请直接写出甲车从B市往回返后再经过几小时两车相遇.
-
科目: 来源: 题型:
查看答案和解析>>【题目】推理填空:如图,点
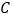 在
在 的一边
的一边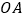 上,过点
上,过点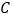 的直线
的直线 平行直线
平行直线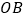 ,
, 平分
平分 ,
,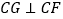 于点
于点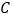 .
.(1)求证:
 平分
平分 ;
;(2)当
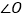 为多少度时,
为多少度时,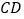 平分
平分 ,并说明理由。
,并说明理由。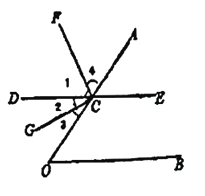
(1)证明:∵
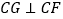 (已知)
(已知)∴
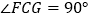 (垂直定义)
(垂直定义)即

又∵
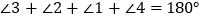 (平角定义)
(平角定义)∴
 ,
,∵
 平分
平分 ,
,∴
 (角平分线定义)
(角平分线定义)∴
 (_____________________)
(_____________________)即
 平分
平分 ;
;(2)解:
 时,
时,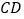 平分
平分 ,理由如下:
,理由如下:∵
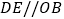 ,
,∴
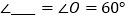 (____________________________),
(____________________________),∴
 _________________°
_________________°又∵
 平分
平分 ,
,∴
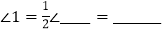 °,
°,∴
 (等量代换)
(等量代换)即
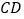 平分
平分 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】下表数据是科研小组在某地区根据调查获取的:“距离地面的高度(千米)与此处的温度(摄氏度)”的关系。
距离地面高度/千米
0
1
2
3
4
5
温度/摄氏度
20
14
8
2
-4
-10
根据上表,请你回答:
(1)上表中___________是自变量;_________________是因变量;
(2)如果用
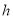 表示距离地面的高度(千米),
表示距离地面的高度(千米),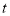 表示温度(摄氏度),请你写出
表示温度(摄氏度),请你写出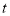 与
与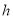 的关系式____________________________________;
的关系式____________________________________;(3)请你利用(2)的结论,求该地区:①距离地面6.2千米的高空温度是多少?②当高空某处温度为-52度时,该处的高度是多少?
相关试题

