【题目】下表数据是科研小组在某地区根据调查获取的:“距离地面的高度(千米)与此处的温度(摄氏度)”的关系。
距离地面高度/千米 | 0 | 1 | 2 | 3 | 4 | 5 |
温度/摄氏度 | 20 | 14 | 8 | 2 | -4 | -10 |
根据上表,请你回答:
(1)上表中___________是自变量;_________________是因变量;
(2)如果用![]() 表示距离地面的高度(千米),
表示距离地面的高度(千米),![]() 表示温度(摄氏度),请你写出
表示温度(摄氏度),请你写出![]() 与
与![]() 的关系式____________________________________;
的关系式____________________________________;
(3)请你利用(2)的结论,求该地区:①距离地面6.2千米的高空温度是多少?②当高空某处温度为-52度时,该处的高度是多少?
参考答案:
【答案】(1)距离地面的高度,温度;(2)![]() ;(3)①距地面6.2千米高空温度为
;(3)①距地面6.2千米高空温度为![]() ;②该处高度为12千米
;②该处高度为12千米
【解析】
(1)函数是指在一个变化过程中的两个变量x、y,对于x的每一个值,y都有唯一的值和它相对应,此时x叫自变量,y叫x的函数;
(2)根据表中数据的变化规律,找到温度和高度之间的关系,列出关系式t=20-6h;
(3)①可直接从表中得到距离地面6.2千米的高空温度;
②将t=-52代入解析式即可求出.
(1)上表反映了温度和距地面高度之间的关系,高度是自变量,温度是因变量.
(2)由表可知,每上升一千米,温度降低6摄氏度,可得解析式为t=20-6h;
(3)①![]() 时,
时,![]()
答:距地面6.2千米高空温度为![]()
②![]() 时,
时,![]()
∴![]()
答:该处高度为12千米。
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明和小亮相约晨练跑步,小明比小亮早1分钟离开家门,3分钟后迎面遇到从家跑来的小亮,两人沿滨江路跑了2分钟后,决定进行长跑比赛,比赛时小明的速度始终是180米/分,小亮的速度始终是220米/分.如图是两人之间的距离y(米)与小明离开家的时间x(分)之间的函数图象,则下列结论中正确的是____________________.(写序号即可)
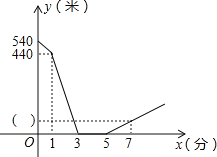
①小明家与小亮家距离为540米;
②小亮比赛前的速度为120米/分;
③小明出发7分钟时,两人距离为80米;
④若小亮从家出门跑了14分钟后,按原路以比赛时的速度返回,则再经过1分钟两人相遇.
-
科目: 来源: 题型:
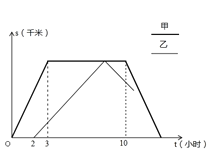
查看答案和解析>>【题目】甲乙两车从A市去往B市,甲比乙出发了2个小时,甲到达B市后停留一段时间返回,乙到达B市后立即返回.甲车往返的速度都为40千米/时,乙车往返的速度都为20千米/时,下图是两车距A市的路程S(千米)与行驶时间t(小时)之间的函数图象,请结合图象回答下列问题:
(1)A、B两市的距离是 千米,甲到B市后 小时乙到达B市;
(2)求甲车返回时的路程s(千米)与时间t(小时)之间的函数关系式,并写出自变量t的取值范围;
(3)请直接写出甲车从B市往回返后再经过几小时两车相遇.
-
科目: 来源: 题型:
查看答案和解析>>【题目】推理填空:如图,点
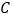 在
在 的一边
的一边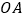 上,过点
上,过点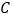 的直线
的直线 平行直线
平行直线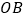 ,
, 平分
平分 ,
,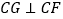 于点
于点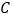 .
.(1)求证:
 平分
平分 ;
;(2)当
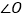 为多少度时,
为多少度时,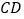 平分
平分 ,并说明理由。
,并说明理由。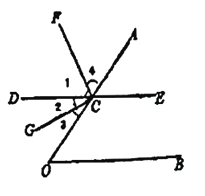
(1)证明:∵
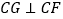 (已知)
(已知)∴
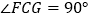 (垂直定义)
(垂直定义)即

又∵
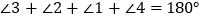 (平角定义)
(平角定义)∴
 ,
,∵
 平分
平分 ,
,∴
 (角平分线定义)
(角平分线定义)∴
 (_____________________)
(_____________________)即
 平分
平分 ;
;(2)解:
 时,
时,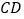 平分
平分 ,理由如下:
,理由如下:∵
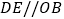 ,
,∴
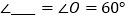 (____________________________),
(____________________________),∴
 _________________°
_________________°又∵
 平分
平分 ,
,∴
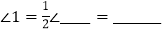 °,
°,∴
 (等量代换)
(等量代换)即
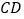 平分
平分 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在长方形
 中,
中, 。点
。点 从
从 出发,沿
出发,沿 路线运动,到
路线运动,到 停止;点
停止;点 出发时的速度为每秒
出发时的速度为每秒 ,7秒时点
,7秒时点 的速度变为每秒
的速度变为每秒 ,图②是点
,图②是点 出发
出发 秒后,
秒后, 的面积
的面积 与
与 (秒)的关系图象;
(秒)的关系图象;
(1)根据题目提供的信息,求出
 的值为______________、
的值为______________、 的值为_________
的值为_________ 的值为___________;
的值为___________;(2)设点
 离开点
离开点 的路程为
的路程为 ,
,①7.5秒时,
 的值为_____________________;
的值为_____________________;②请求出当动点
 改变速度后,
改变速度后, 与
与 的关系式;
的关系式;(3)点
 出发后几秒,
出发后几秒, 的面积
的面积 是长方形
是长方形 面积的
面积的 ?并说明理由。
?并说明理由。 -
科目: 来源: 题型:
查看答案和解析>>【题目】定义:在平面直角坐标系中,对于任意两点
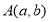 ,
,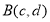 ,若点
,若点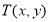 满足
满足 ,
,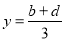 ,那么称点
,那么称点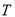 是点
是点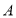 ,
,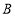 的融合点.
的融合点.例如:
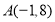 ,
,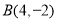 ,当点
,当点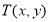 满是
满是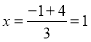 ,
, 时,则点
时,则点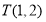 是点
是点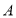 ,
,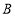 的融合点,
的融合点,
(1)已知点
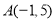 ,
,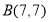 ,
,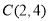 ,请说明其中一个点是另外两个点的融合点.
,请说明其中一个点是另外两个点的融合点.(2)如图,点
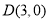 ,点
,点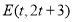 是直线
是直线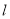 上任意一点,点
上任意一点,点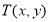 是点
是点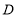 ,
,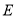 的融合点.
的融合点.①试确定
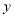 与
与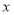 的关系式.
的关系式.②若直线
 交
交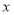 轴于点
轴于点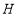 ,当
,当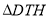 为直角三角形时,求点
为直角三角形时,求点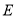 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AD平分∠CAB.
(1)求∠CAD的度数;
(2)延长AC至E,使CE=AC,求证:DA=DE.

相关试题

