【题目】请阅读下列材料:
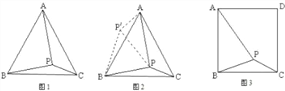
问题:如图1,在等边三角形ABC内有一点P,且PA=2,PB=![]() ,PC=1、求∠BPC度数的大小和等边三角形ABC的边长.
,PC=1、求∠BPC度数的大小和等边三角形ABC的边长.
李明同学的思路是:将△BPC绕点B逆时针旋转60°,画出旋转后的图形(如图2),连接PP′,可得△P′PB是等边三角形,而△PP′A又是直角三角形(由勾股定理的逆定理可证),所以∠AP′B=150°,而∠BPC=∠AP′B=150°,进而求出等边△ABC的边长为![]() ,问题得到解决.
,问题得到解决.
请你参考李明同学的思路,探究并解决下列问题:如图3,在正方形ABCD内有一点P,且PA=![]() ,BP=
,BP=![]() ,PC=1.求∠BPC度数的大小和正方形ABCD的边长.
,PC=1.求∠BPC度数的大小和正方形ABCD的边长.
参考答案:
【答案】(1)135°;(2)![]() ;
;
【解析】试题分析:
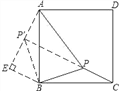
(1)如图,将△BPC绕点B逆时针旋转90°,得△BP′A,则△BPC≌△BP′A,由此可得:AP′=PC=1,BP=BP′=![]() ;连接PP′,由∠PBP′=90°可得PP′=2,∠BP′P=45°,这样在△AP′P中由勾股定理的逆定理可得∠AP′P=90°,从而可得∠AP′B=135°,由此可得∠BPC=∠AP′B=135°;
;连接PP′,由∠PBP′=90°可得PP′=2,∠BP′P=45°,这样在△AP′P中由勾股定理的逆定理可得∠AP′P=90°,从而可得∠AP′B=135°,由此可得∠BPC=∠AP′B=135°;
(2)过点B作BE⊥AP′,交AP′的延长线于点E,结合(1)中∠AP′B=135°可证得△BEP′是等腰直角三角形,结合BP′=![]() ,可得EP′=BE=1,从而可得AE=2,结合BE=1在Rt△ABE中由勾股定理即可求得AB的长.
,可得EP′=BE=1,从而可得AE=2,结合BE=1在Rt△ABE中由勾股定理即可求得AB的长.
试题解析:
(1)如图,
将△BPC绕点B逆时针旋转90°,得△BP′A,则△BPC≌△BP′A.
∴AP′=PC=1,BP=BP′=![]() ;
;
连接PP′,
在Rt△BP′P中,
∵BP=BP′=![]() ,∠PBP′=90°,
,∠PBP′=90°,
∴PP′=2,∠BP′P=45°;
在△AP′P中,AP′=1,PP′=2,AP=![]() ,
,
∵![]() ,即AP′2+PP′2=AP2;
,即AP′2+PP′2=AP2;
∴△AP′P是直角三角形,即∠AP′P=90°,
∴∠AP′B=135°,
∴∠BPC=∠AP′B=135°.
(2)过点B作BE⊥AP′,交AP′的延长线于点E,
∴∠BEP′=90°,
∵∠AP′B=135°,
∴∠EP′B=45°,
∴△BEP′是等腰直角三角形,
∵BP′=![]() ,
,
∴EP′=BE=1,
∴AE=AP′+EP′=2;
∴在Rt△ABE中,由勾股定理,得AB=![]() ;
;
∴∠BPC=135°,正方形边长为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一个正方体的表面涂上颜色.如图把正方体的棱
 等分,然后沿等分线把正方体切开,能够得到
等分,然后沿等分线把正方体切开,能够得到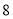 个小正方体,通过观察我们可以发现
个小正方体,通过观察我们可以发现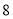 个小正方体全是
个小正方体全是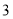 个面涂有颜色的.如果把正方体的棱三等分,然后沿等分线把正方体切开,能够得到
个面涂有颜色的.如果把正方体的棱三等分,然后沿等分线把正方体切开,能够得到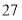 个小正方体,通过观察我们可以发现这些小正方体中有
个小正方体,通过观察我们可以发现这些小正方体中有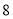 个是
个是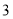 个面涂有颜色的,有
个面涂有颜色的,有 个是
个是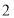 个面涂有颜色的,有
个面涂有颜色的,有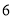 个是
个是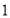 个面涂有颜色的,还有
个面涂有颜色的,还有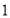 个各个面都没有涂色.
个各个面都没有涂色.
(1)如果把正方体的棱
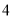 等分,所得小正方体表面涂色情况如何呢?把正方体的棱
等分,所得小正方体表面涂色情况如何呢?把正方体的棱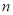 等分呢?(请填写下表):
等分呢?(请填写下表):棱等分数
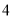 等分
等分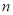 等分
等分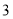 面涂色的正方体
面涂色的正方体___________个
_____________个
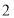 面涂色的正方体
面涂色的正方体__________个
____________个
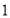 面涂色的正方体
面涂色的正方体___________个
____________个
各个面都无涂色的正方体
___________个
____________个
(2)请直接写出将棱
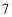 等分时只有一个面涂色的小正方体的个数_____________.
等分时只有一个面涂色的小正方体的个数_____________. -
科目: 来源: 题型:
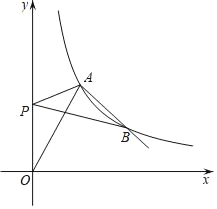
查看答案和解析>>【题目】如图,函数y=
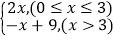 的图象与双曲线y=
的图象与双曲线y=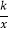 (k≠0,x>0)相交于点A(3,m)和点B.
(k≠0,x>0)相交于点A(3,m)和点B.(1)求双曲线的解析式及点B的坐标;
(2)若点P在y轴上,连接PA,PB,求当PA+PB的值最小时点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】嫦娥四号探测器于2019年1月3日,成功着陆在月球背面,通过“鹊桥”中继星传回了世界第一张近距离拍摄的月背影像图,开启了人类月球探测新篇章.当中继星成功运行于地月拉格朗日L2点时,它距离地球约1500000km.用科学记数法表示数1500000为( )

A.15×105 B.1.5×106C.0.15×107D.1.5×105
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,
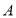 、
、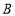 在数轴上对应的数分别用
在数轴上对应的数分别用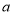 、
、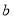 表示,且
表示,且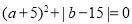 .
.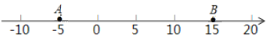
(1)数轴上点
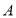 表示的数是________,点
表示的数是________,点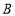 表示的数是___________;
表示的数是___________;(2)若一动点
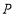 从点
从点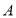 出发,以
出发,以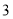 个单位长度秒速度由
个单位长度秒速度由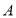 向
向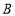 运动;动点
运动;动点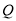 从原点
从原点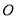 出发,以
出发,以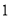 个单位长度
个单位长度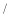 秒速度向
秒速度向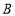 运动,点
运动,点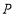 、
、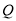 同时出发,点
同时出发,点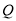 运动到
运动到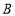 点时两点同时停止.设点
点时两点同时停止.设点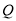 运动时间为
运动时间为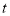 秒.
秒.①若
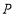 从
从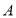 到
到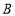 运动,则
运动,则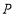 点表示的数为_______,
点表示的数为_______,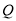 点表示的数为___________(用含
点表示的数为___________(用含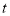 的式子表示)
的式子表示)②当
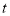 为何值时,点
为何值时,点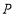 与点
与点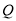 之间的距离为
之间的距离为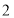 个单位长度.
个单位长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,∠B=30°,以点A为圆心,任意长为半径画弧分别交AB,AC于点M和N,再分别以点M,N为圆心画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
①AD是∠BAC的平分线
②∠ADC=60°
③△ABD是等腰三角形
④点D到直线AB的距离等于CD的长度.
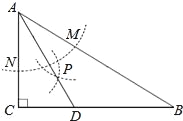
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明在家中利用物理知识称量某个品牌纯牛奶的净含量,称得六盒纯牛奶的含量分别为:248mL,250mL,249mL,251mL,249mL,253mL,对于这组数据,下列说法正确的是( ).
A.平均数为251mL B.中位数为249mL
C.众数为250mL D.方差为

相关试题

