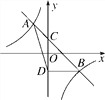
【题目】如图,一次函数y=k1x+b与反比例函数y=![]() (k2≠0)相交于A(-1,2),B(2,m)两点,与y轴相交于点C.
(k2≠0)相交于A(-1,2),B(2,m)两点,与y轴相交于点C.
(1)求k1、k2、m的值;
(2)若点D与点C关于x轴对称,求△ABD的面积;
(3)若M(x1,y1)、N(x2、y2)是反比例函数y=![]() 图象上的两点,且x1<x2时,y1>y2,指出点M、N各位于坐标系的哪个象限,并简要说明理由.
图象上的两点,且x1<x2时,y1>y2,指出点M、N各位于坐标系的哪个象限,并简要说明理由.
参考答案:
【答案】(1)![]() ;(2) 3;(3)当点M在第二象限,点N在第四象限时,满足当x1<x2时,y1>y2.
;(2) 3;(3)当点M在第二象限,点N在第四象限时,满足当x1<x2时,y1>y2.
【解析】(1)把A的坐标代入y=![]() 即可求得k2,得到反比例函数的解析式,再把B(2,m)代入反比例函数的解析式即可求得m的值,然后根据待定系数法即可求得k1;
即可求得k2,得到反比例函数的解析式,再把B(2,m)代入反比例函数的解析式即可求得m的值,然后根据待定系数法即可求得k1;
(2)根据一次函数的解析式求得点C的坐标,根据题意求得D的坐标,从而求得DB∥x轴,BD=2,然后根据三角形,、面积公式求得即可;
(3)根据反比例函数的性质即可判断.
(1)∵比例函数y=![]() 经过A(-1,2),
经过A(-1,2),
∴k2=-2,
∴比例函数为y=-![]() ,
,
∵B(2,m)在比例函数y=-![]() 的图象上,
的图象上,
∴m=-![]() =-1,
=-1,
∴B(2,-1),
∵直线y=k1x+b经过A(-1,2),B(2,-1),
∴![]() ,解得k1=-1,b=1,
,解得k1=-1,b=1,
(2)由直线y=-x+1可知C(0,1),
∵点D与点C关于x轴对称,
∴D(0,-1),
∵B(2,-1),
∴BD∥x轴,BD=2,
∴△ABD的面积=![]() ×2×(2+1)=3;
×2×(2+1)=3;
(3)点M位于第二象限,N位于第四象限,
∵k2=-2<0,图象位于二、四象限,在每个象限内,y随x的增大而增大,
∴如果M(x1,y1)、N(x2,y2)位于同一象限,有且x1<x2时,则y1<y2,
∴M(x1,y1)、N(x2,y2)位于不同的象限,
∵x1<x2,
∴点M位于第二象限,N位于第四象限.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算下列各题
(1)计算: ﹣(3﹣π)0﹣|﹣3+2|;
﹣(3﹣π)0﹣|﹣3+2|;
(2)计算: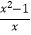 ÷(1+
÷(1+  )
) -
科目: 来源: 题型:
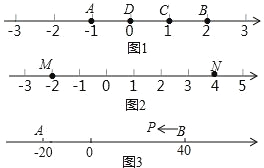
查看答案和解析>>【题目】A、B、C 为数轴上三点,若点 C 到点 A 的距离是点 C 到点 B 的距离的 2倍,则称点 C 是(A,B)的奇异点,例如图 1 中,点 A 表示的数为﹣1,点B 表示的数为 2,表示 1 的点 C 到点 A 的距离为 2,到点 B 的距离为 1,则点C 是(A,B)的奇异点,但不是(B,A)的奇异点.
(1)在图 1 中,直接说出点 D 是(A,B)还是(B,C)的奇异点;
(2)如图 2,若数轴上 M、N 两点表示的数分别为﹣2 和 4,(M,N)的奇异点 K 在 M、N 两点之间,请求出 K 点表示的数;
(3)如图 3,A、B 在数轴上表示的数分别为﹣20 和 40,现有一点 P 从点 B 出发,向左运动.
①若点 P 到达点 A 停止,则当点 P 表示的数为多少时,P、A、B 中恰有一个点为其余两点的奇异点?
②若点 P 到达点 A 后继续向左运动,是否存在使得 P、A、B 中恰有一个点为其余两点的奇异点的情况?若存在,请直接写出此时 PB 的距离;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程与不等式组
(1)解方程:x2+4x﹣5=0;
(2)解不等式组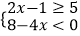 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某食品厂从生产的袋装食品中抽出样品20袋,检测每袋的重量是否符合标准,超过或不足的部分分别用正、负数来表示,记录如下表:
与标准重量的差值(单位:g)
﹣5
﹣2
0
1
3
6
袋数
1
4
3
4
5
3
(1)计算这批样品的平均重量,判断它比标准重量重还是轻多少?
(2)若标准重量为450克,则这批样品的总重量是多少?
(3)若这种食品的合格标准为450±5克,则这批样品的合格率为 (直接填写答案)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,连接CE,连接DE交AC于F,AD=4,AB=6.
(1)求证:△ADC∽△ACB;
(2)求AC的值;
(3)求
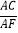 的值.
的值.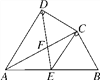
-
科目: 来源: 题型:
查看答案和解析>>【题目】“十一”国庆期间出租车司机小李某天下午的营运始终在长安街(自东向西或自西向东)上进行,如果规定向东为正,向西为负,他这天下午从天安门出发,行车里程(单位:千米)如下:
+15,﹣2,+5,﹣1,+10,﹣3,﹣2,+12,+4,﹣5,+6.
(1)小李将最后一名乘客送抵目的地时,小李距天安门有多远?
(2)如果汽车耗油量为0.08升/千米,这天下午小李共耗油多少升?
相关试题

