搜索
【题目】解方程与不等式组
（1）解方程：x2+4x﹣5=0；
（2）解不等式组 
．
参考答案：
【答案】
（1）解：原方程变形为（x﹣1）（x+5）=0，
所以x1=﹣5，x2=1
（2）解： 
，
由①得：x≥3，
由②得：x＞2，
所以不等式组的解集为：x≥3
【解析】（1）利用因式分解法求解即可；（2）先解不等式组中的每一个不等式，再求其公共解集即可．
【考点精析】利用一元一次不等式组的解法对题目进行判断即可得到答案，需要熟知解法：①分别求出这个不等式组中各个不等式的解集；②利用数轴表示出各个不等式的解集；③找出公共部分；④用不等式表示出这个不等式组的解集．如果这些不等式的解集的没有公共部分，则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 )．
-
科目： 来源： 题型：
查看答案和解析>>【题目】小文同学每天乘从BRT(城市快速公交)上学，为了方便乘坐BRT，他用自己勤工俭学的钱买了80元的公交卡．如果他乘坐的次数用n表示，则记录他每次乘坐BRT后公交卡的余额(单位：元)如下表：
次数n
余额(元)
1
80-0.9
2
80-1.8
3
80-2.7
4
80-3.6
…
…
(1)写出用乘坐BRT的次数n表示余额的式子为____________________；
(2)利用(1)中的式子，帮助小文同学算一算，他一个月乘坐BRT有84次，这80元的公交卡够不够用，若够用，能剩多少元？
(3)小文同学用80元的公交卡最多能乘坐BRT__________________次．
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算下列各题
（1）计算：
﹣（3﹣π）0﹣|﹣3+2|；
（2）计算：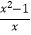
÷（1+ 
） -
科目： 来源： 题型：
查看答案和解析>>【题目】A、B、C 为数轴上三点，若点 C 到点 A 的距离是点 C 到点 B 的距离的 2倍，则称点 C 是（A，B）的奇异点，例如图 1 中，点 A 表示的数为﹣1，点B 表示的数为 2，表示 1 的点 C 到点 A 的距离为 2，到点 B 的距离为 1，则点C 是（A，B）的奇异点，但不是（B，A）的奇异点．
(1)在图 1 中，直接说出点 D 是（A，B）还是（B，C）的奇异点；
(2)如图 2，若数轴上 M、N 两点表示的数分别为﹣2 和 4，（M，N）的奇异点 K 在 M、N 两点之间，请求出 K 点表示的数；
(3)如图 3，A、B 在数轴上表示的数分别为﹣20 和 40，现有一点 P 从点 B 出发，向左运动．
①若点 P 到达点 A 停止，则当点 P 表示的数为多少时，P、A、B 中恰有一个点为其余两点的奇异点？
②若点 P 到达点 A 后继续向左运动，是否存在使得 P、A、B 中恰有一个点为其余两点的奇异点的情况？若存在，请直接写出此时 PB 的距离；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一次函数y＝k1x＋b与反比例函数y＝
(k2≠0)相交于A(－1，2)，B(2，m)两点，与y轴相交于点C.(1)求k1、k2、m的值；
(2)若点D与点C关于x轴对称，求△ABD的面积；
(3)若M(x1，y1)、N(x2、y2)是反比例函数y＝
图象上的两点，且x1<x2时，y1>y2，指出点M、N各位于坐标系的哪个象限，并简要说明理由．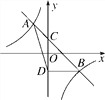
-
科目： 来源： 题型：
查看答案和解析>>【题目】某食品厂从生产的袋装食品中抽出样品20袋，检测每袋的重量是否符合标准，超过或不足的部分分别用正、负数来表示，记录如下表：
与标准重量的差值（单位：g）
﹣5
﹣2
0
1
3
6
袋数
1
4
3
4
5
3
（1）计算这批样品的平均重量，判断它比标准重量重还是轻多少？
（2）若标准重量为450克，则这批样品的总重量是多少？
（3）若这种食品的合格标准为450±5克，则这批样品的合格率为 （直接填写答案）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，四边形ABCD中，AC平分∠DAB，∠ADC＝∠ACB＝90°，E为AB的中点，连接CE，连接DE交AC于F，AD＝4，AB＝6.
(1)求证：△ADC∽△ACB；
(2)求AC的值；
(3)求
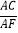的值．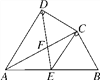
相关试题
