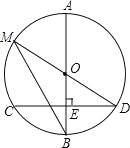
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点E,且CD=24,点M在⊙O上,MD经过圆心O,联结MB.
(1)若BE=8,求⊙O的半径;
(2)若∠DMB=∠D,求线段OE的长.
参考答案:
【答案】(1)13;
(2)OE=4![]() .
.
【解析】
试题分析:(1)根据垂径定理求出DE的长,设出半径,根据勾股定理,列出方程求出半径;
(2)根据OM=OB,证出∠M=∠B,根据∠M=∠D,求出∠D的度数,根据锐角三角函数求出OE的长.
试题解析:(1)设⊙O的半径为x,则OE=x﹣8,
∵CD=24,由垂径定理得,DE=12,
在Rt△ODE中,OD2=DE2+OE2,
x2=(x﹣8)2+122,
解得:x=13.
(2)∵OM=OB,
∴∠M=∠B,
∴∠DOE=2∠M,
又∠M=∠D,
∴∠D=30°,
在Rt△OED中,∵DE=12,∠D=30°,
∴OE=4![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把抛物线y=﹣x2向左平移1个单位,然后向上平移3个单位,则平移后抛物线的解析式为( )
A.y=﹣(x﹣1)2﹣3B.y=﹣(x+1)2﹣3
C.y=﹣(x﹣1)2+3D.y=﹣(x+1)2+3
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分11分)如果一个三角形能被一条线段分割成两个等腰三角形,那么称这条线段为这个三角形的特异线,称这个三角形为特异三角形.
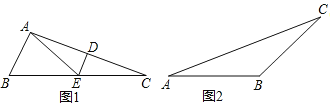
(1)如图1,△ABC中,∠B=2∠C,线段AC的垂直平分线交AC于点D,交BC于点E.求证:AE是△ABC的一条特异线;
(2)如图2,若△ABC是特异三角形,∠A=30°,∠B为钝角,求出所有可能的∠B的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】巴黎与东京的时差为-8,带正号的数表示同一时间比东京早的时间数.如果东京现在的时间是13:20.那么巴黎现在的时间是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】将直角三角形的三条边长同时扩大同一倍数, 得到的三角形是( )
A. 钝角三角形 B. 锐角三角形 C. 直角三角形 D. 等腰三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的一元二次方程x2﹣2x﹣k=0没有实数根,则k的取值范围是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】将抛物线y=x2﹣2x+3向上平移2个单位长度,再向右平移3个单位长度后,得到的抛物线的解析式为( )
A.y=(x﹣1)2+4B.y=(x﹣4)2+4C.y=(x+2)2+6D.y=(x﹣4)2+6
相关试题

