【题目】为了鼓励市民节约用水,某市自来水公司对每户用水量进行了分段计费,每户每月用水量在规定吨数以下的收费标准相同,规定吨数以上的超过部分收费相同.如表是小明家1﹣4月用水量和交费情况:
月份 | 1 | 2 | 3 | 4 |
用水量(吨) | 6 | 8 | 12 | 15 |
费用(元) | 12 | 16 | 28 | 37 |
(Ⅰ)若小明家5月份用水25吨,则应缴多少元水费?
(Ⅱ)若该户居民某月份用水为![]() 吨,则应收水费多少元?(用含
吨,则应收水费多少元?(用含![]() 的代数式表示,并化简).
的代数式表示,并化简).
参考答案:
【答案】(Ⅰ)应缴水费67元;(Ⅱ)应收水费![]() 元或
元或![]() 元.
元.
【解析】
(Ⅰ)由小明家1,2月份的用水情况,可求出规定用量内的收费标准;由小明家3,4月份的用水情况,可求出超过部分的收费标准;设该市规定用水量为x吨,由小明家3月份用水12吨缴纳28元,即可得出关于x的一元一次方程,解之即可得出结论;
(Ⅱ)分类讨论:当0≤x≤8时或当x>8时,分别计算水费即可.
(Ⅰ)∵12÷6=2(元/吨),16÷8=2(元/吨),
∴规定用量内的收费标准是2元/吨.
∵12×2=24(元),24<28,
∴规定的用水量小于12吨,
∴超过部分的收费标准是(37-28)÷(15-12)=3(元/吨).
设该市规定用水量为x吨,
依题意,得:2x+3(12-x)=28,
解得:x=8.
∴该市规定用水量为8吨,
小明家5月份用水25吨,则应缴水费为:
![]()
![]()
![]() (元)
(元)
答:应缴水费67元;
(Ⅱ)由题意得:
当![]() 时,应缴水费为:
时,应缴水费为:![]() (元);
(元);
当![]() 时,应缴水费为:
时,应缴水费为:![]() (元)
(元)
答:应收水费![]() 元或
元或![]() 元.
元.
-
科目: 来源: 题型:
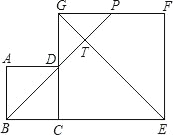
查看答案和解析>>【题目】如图,边长分别为4和8的两个正方形ABCD和CEFG并排放在一起,连结BD并延长交EG于点T,交FG于点P,则GT的长为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义运算max{a,b}:当a≥b时,max{a,b}=a;当a<b时,max{a,b}=b.如max{﹣3,2}=2.
(1)max{
 ,3}= ;
,3}= ;(2)已知y1=
 和y2=k2x+b在同一坐标系中的图象如图所示,若max{
和y2=k2x+b在同一坐标系中的图象如图所示,若max{ ,k2x+b}=
,k2x+b}= ,结合图象,直接写出x的取值范围;
,结合图象,直接写出x的取值范围;(3)用分类讨论的方法,求max{2x+1,x﹣2}的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,点D在BC上,BD=DC,过点D作DE⊥AC,垂足为E,⊙O经过A,B,D三点.
(1)求证:AB是⊙O的直径;
(2)判断DE与⊙O的位置关系,并加以证明;
(3)若⊙O的半径为3,∠BAC=60°,求DE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形
 中,
中, ,
, 是
是 中点,
中点, 在
在 延长线上,连接
延长线上,连接 相交于点
相交于点 .
. 
(1)若
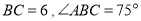 ,求平行四边形
,求平行四边形 的面积;
的面积;(2)若
 ,求证:
,求证: .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上点A表示的数为6,B是数轴上在左侧的一点,且A,B两点间的距离为10。动点P从点A出发,以每秒6个单位长度的度沿数轴向左匀速运动,设运动时间为t
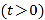 秒。
秒。
(1)数轴上点B表示的数是______;当点P运动到AB的中点时,它所表示的数是_____。
(2)动点Q从点B出发,以每秒2个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发,求:
①当点P运动多少秒时,点P追上点Q?
②当点P运动多少秒时,点P与点Q间的距离为8个单位长度?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某集团公司对所属甲、乙两分厂下半年经营情况记录(其中“+”表示盈利,“-”表示亏损,单位:亿元)如下表.
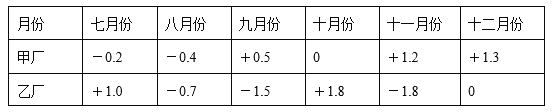
(1)计算八月份乙厂比甲厂多亏损多少亿元?
(2)分别计算下半年甲、乙两个工厂平均每月盈利或亏损多少亿元?
相关试题

