【题目】已知数轴上点A表示的数为6,B是数轴上在左侧的一点,且A,B两点间的距离为10。动点P从点A出发,以每秒6个单位长度的度沿数轴向左匀速运动,设运动时间为t![]() 秒。
秒。
![]()
(1)数轴上点B表示的数是______;当点P运动到AB的中点时,它所表示的数是_____。
(2)动点Q从点B出发,以每秒2个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发,求:
①当点P运动多少秒时,点P追上点Q?
②当点P运动多少秒时,点P与点Q间的距离为8个单位长度?
参考答案:
【答案】(1)-4,1(2)①当点P运动2.5秒时,点P追上点Q;②当点P运动0.5秒或4.5秒时,点P与点Q间的距离为8个单位长度.
【解析】
(1)由已知得OA=6,则OB=AB-OA=4,写出数轴上点B所表示的数;根据点P运动到AB的中点,即可得出P点所表示的数:
(2)①设点P运动t秒时追上点Q,根据等量关系得到6t-2t=10,然后求解即可;
②分点P未超过点Q和点P超过点Q两种情况讨论,设运动时间为m,根据题意得到当P不超过Q,则(6-6m )-(-4-2m)=8,当P超过Q,则(-4-2m)-(6-6m )=8,求解即可.
解:(1)∵数轴上点A表示的数为6,
∴OA=6,
则OB=AB-OA=10-6=4,
点B在原点左边,
∴数轴上点B所表示的数为-4;
∵数轴上点A表示的数为6,数轴上点B所表示的数为-4
∴AB的中点是:1
∴数轴上点P所表示的数为:1
故答案为:-4,1
(2)①设点P运动t秒时追上点Q,
则6t-2t=10,
解得t=2.5,
所以当点P运动2.5秒时,点P追上点Q;
②设当点P运动m秒时,点P与点Q间的距离为8个单位长度,数轴上点P所表示的数为:6-6m,数轴上点Q所表示的数为:-4-2m,
当P不超过Q,则(6-6m )-(-4-2m)=8,解得m=0.5;
当P超过Q,则(-4-2m)-(6-6m )=8,解得m=4.5;
所以当点P运动0.5秒或4.5秒时,点P与点Q间的距离为8个单位长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,点D在BC上,BD=DC,过点D作DE⊥AC,垂足为E,⊙O经过A,B,D三点.
(1)求证:AB是⊙O的直径;
(2)判断DE与⊙O的位置关系,并加以证明;
(3)若⊙O的半径为3,∠BAC=60°,求DE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了鼓励市民节约用水,某市自来水公司对每户用水量进行了分段计费,每户每月用水量在规定吨数以下的收费标准相同,规定吨数以上的超过部分收费相同.如表是小明家1﹣4月用水量和交费情况:
月份
1
2
3
4
用水量(吨)
6
8
12
15
费用(元)
12
16
28
37
(Ⅰ)若小明家5月份用水25吨,则应缴多少元水费?
(Ⅱ)若该户居民某月份用水为
 吨,则应收水费多少元?(用含
吨,则应收水费多少元?(用含 的代数式表示,并化简).
的代数式表示,并化简). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形
 中,
中, ,
, 是
是 中点,
中点, 在
在 延长线上,连接
延长线上,连接 相交于点
相交于点 .
. 
(1)若
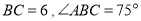 ,求平行四边形
,求平行四边形 的面积;
的面积;(2)若
 ,求证:
,求证: .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某集团公司对所属甲、乙两分厂下半年经营情况记录(其中“+”表示盈利,“-”表示亏损,单位:亿元)如下表.
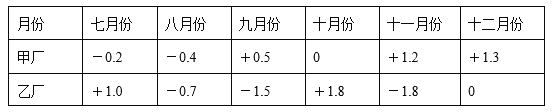
(1)计算八月份乙厂比甲厂多亏损多少亿元?
(2)分别计算下半年甲、乙两个工厂平均每月盈利或亏损多少亿元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们规定,若关于
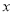 的一元一次方程
的一元一次方程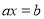 的解为
的解为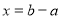 ,则称该方程为“奇异方程”.例如:
,则称该方程为“奇异方程”.例如: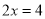 的解为
的解为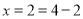 ,则该方程
,则该方程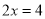 是“奇异方程”.请根据上述规定解答下列问题:
是“奇异方程”.请根据上述规定解答下列问题:(Ⅰ)判断方程
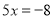 ________(回答“是”或“不是”)“奇异方程”;
________(回答“是”或“不是”)“奇异方程”;(Ⅱ)若
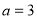 ,有符合要求的“奇异方程”吗?若有,求
,有符合要求的“奇异方程”吗?若有,求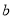 的值;若没有,请说明理由.
的值;若没有,请说明理由.(Ⅲ)若关于
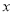 的一元一次方程
的一元一次方程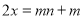 和
和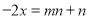 都是“奇异方程”,求代数式
都是“奇异方程”,求代数式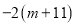 +
+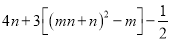
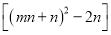 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中的每个小正方形边长为1,△ABC的顶点在网格的格点上.
(1)画线段AD∥BC,且使AD=BC,连接BD;此时D点的坐标是 .
(2)直接写出线段AC的长为 ,AD的长为 ,BD的长为 .
(3)直接写出△ABD为 三角形,四边形ADBC面积是 .

相关试题

