【题目】如图,Rt△ABC中,∠A=60°,将△ABC绕点C顺时针旋转得到△A1B1C,斜边A1B1与CB相交于点D,且DC=AC,则旋转角∠ACA1等于( ) 
A.20°
B.25°
C.30°
D.35°
参考答案:
【答案】C
【解析】解:∵△ABC绕点C顺时针旋转得到△A1B1C,
∴∠A1=∠A=60°,CA1=CA,
∵DC=AC,
∴CA1=CD,
∴△A1CD为等边三角形,
∴∠A1CD=60°,
∴∠ACA1=∠ACB﹣∠A1CD=90°﹣60°=30°.
故选C.
【考点精析】关于本题考查的旋转的性质,需要了解①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,经过点A(0,﹣4)的抛物线y=
 x2+bx+c与x轴相交于点B(﹣1,0)和C,O为坐标原点.
x2+bx+c与x轴相交于点B(﹣1,0)和C,O为坐标原点.
(1)求抛物线的解析式;
(2)将抛物线y= x2+bx+c向上平移
x2+bx+c向上平移  个单位长度,再向左平移m(m>0)个单位长度,得到新抛物线,若新抛物线的顶点P在△ABC内,求m的取值范围;
个单位长度,再向左平移m(m>0)个单位长度,得到新抛物线,若新抛物线的顶点P在△ABC内,求m的取值范围;
(3)将x轴下方的抛物线图象关于x轴对称,得到新的函数图象C,若直线y=x+k与图象C始终有3个交点,求满足条件的k的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的二次函数y═ax2+bx+c的图象,下列结论:①b2﹣4ac>0;②c>1;③2a﹣b<0;④a+b+c<0,其中正确的有( )
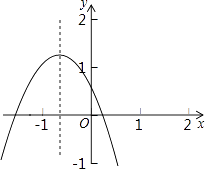
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,正确的有( )
①射线
 和射线
和射线 是同一条射线.②将一根细木条固定在墙上,至少需要钉两个钉子,其理论依据是:两点之间线段最短.③两点间的连线的长度叫做这两点间的距离.
是同一条射线.②将一根细木条固定在墙上,至少需要钉两个钉子,其理论依据是:两点之间线段最短.③两点间的连线的长度叫做这两点间的距离.④表示北偏东
 方向、南偏东
方向、南偏东 方向的两条射线所夹的角为直角.
方向的两条射线所夹的角为直角.A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为2,E是CD的中点,将△ADE绕点A按顺时针方向旋转后得到△ABF,则EF的长等于( )
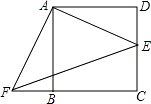
A.3
B.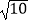
C.2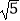
D.3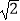
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=x2+bx图象的对称轴为直线x=1,若关于x的一元二次方程x2+bx﹣t=0(t为实数)在﹣1≤x≤3的范围内有解,则t的取值范围是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. 画出
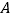 、
、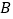 两点间的距离 B. 连接两点之间的直线的长度叫做选两点间的距离
两点间的距离 B. 连接两点之间的直线的长度叫做选两点间的距离C. 线段的大小关系与它们的长度的大小关系是一致的 D. 若
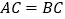 ,则
,则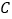 必定是线段
必定是线段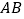 的中点
的中点
相关试题

