Question

【题目】已知二次函数y=x2﹣2x﹣3与x轴交于A、B两点（A在B的左边），与y轴交于点C．

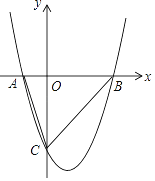
（1）求出点A、B、C的坐标．

（2）求S△ABC

（3）在抛物线上（除点C外），是否存在点N，使得S△NAB=S△ABC ， 若存在，求出点N的坐标，若不 存在，请说明理由．

Answer 1

【答案】（1）A（﹣1，0）、B（3，0）；（2）6；（3）存在，点N的坐标（1+ ，3）或（1﹣，3）或（2，﹣3）

【解析】试题分析：

（1）在解析式中，由，求得的对应值可得点C的坐标；由，求得对应的的值可得点A、B的坐标；

（2）根据（1）中所求点A、B、C坐标可求得△ABC的面积；

（3）设点N的纵坐标为，则由S△NAB=S△ABC可知或，由点N在抛物线上，可得或，解方程即可求得点N的横坐标，从而得到点N的坐标.

试题解析：

（1）在中，当时，，

∴点C的坐标为：（0，﹣3），

当时，，解得：，

∴点A的坐标为：（﹣1，0）、点B的坐标为：（3，0）；

（2）∵点A的坐标为：（﹣1，0）、点B的坐标为：（3，0），

∴AB=3+1=4，

∵点C的坐标为：（0，﹣3），

∴OC=3，

∴S△ABC= ABOC=×4×3=6；

（3）存在点N，使S△NAB=S△ABC，

设点N的纵坐标为，

∵S△NAB=S△ABC，OC=3，

∴或，

∴或，

解得：或，

∵点N不与点C重合，

∴点N的坐标为：（1+，3）或（1﹣，3）或（2，﹣3）.