Question

【题目】如图，在Rt△ABC 中，∠C=90°，AB=15，BC=9，点P，Q分别在BC，AC上，CP=3x，CQ=4x（0＜x＜3）．把△PCQ绕点P旋转，得到△PDE，点D落在线段PQ上．

（1）求证：PQ∥AB；

（2）若点D在BAC的平分线上，求CP的长；

（3）若△PDE与△ABC重叠部分图形的周长为T，且12≤T≤16，求x的取值范围．

Answer 1

【答案】（1）证明见解析（2）6（3）1≤x≤

【解析】试题分析：

（1）由已知条件易证，结合∠C=∠C，可证△PQC∽△BAC，，从而可得∠CPQ=∠B，就可得到PQ∥AB；
（2）连接AD，由AD平分∠BAC和PQ∥AB，易证AQ=DQ，再用含“”的式子表达出AQ和DQ列出方程可求得的值；

（3）由题意可知：点E可能在△ABC内部，也可能在△ABC外部，还可能在AB边上，先取点E在AB边上这一特殊情况讨论得到一个的值，再去讨论另两种情况；①当点E在AB上时，利用折叠的性质和PQ∥AB易证PB=PE=PC=，再由PC+PB=可解得，此时对应的T=；然后再分点E在△ABC内部和外部进行讨论可得符合要求的的取值范围.

试题解析：

（1）∵在Rt△ABC中，AB=15，BC=9，

∴AC=，

∵，

∴，

∵∠C=∠C，
∴△PQC∽△BAC，
∴∠CPQ=∠B，
∴PQ∥AB.
（2）连接AD，∵PQ∥AB，
∴∠ADQ=∠DAB．
∵点D在∠BAC的平分线上，
∴∠DAQ=∠DAB，
∴∠ADQ=∠DAQ，
∴AQ=DQ．
在Rt△CPQ中，PQ=5x，
∵PD=PC=3x，
∴DQ=2x．
∵AQ=12﹣4x，
∴12﹣4x=2x，解得x=2，
∴CP=3x=6．

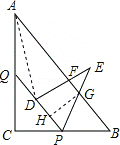
（3）当点E在AB上时，
∵PQ∥AB，
∴∠DPE=∠PEB．
∵∠CPQ=∠DPE，∠CPQ=∠B，
∴∠B=∠PEB，
∴PB=PE=5x，
∴3x+5x=9，解得x=．
①当0＜x<时，点E在△ABC的内部，T=PD+DE+PE=3x+4x+5x=12x，此时0＜T<；
②当＜x＜3时，点E在△ABC的外部，设PE交AB于点G，DE交AB于F，作GH⊥FQ，垂足为H，
∴HG=DF，FG=DH，Rt△PHG∽Rt△PDE，
∴，
∵PG=PB=9﹣3x，
∴，
∴GH= (9﹣3x)，PH= (9﹣3x)，
∴FG=DH=3x﹣ (9﹣3x)，
∴T=PG+PD+DF+FG=(9﹣3x)+3x+ (9﹣3x)+[3x﹣ (9﹣3x)]=，
此时， ＜T＜18．
∴当0＜x＜3时，T随x的增大而增大，
∴T=12时，即12x=12，解得x=1；
T=16时，即=16，解得x=．
∵12≤T≤16，
∴x的取值范围是1≤x≤．