【题目】如图,在Rt△ABC中,![]() ,
,![]() 角平分线交BC于O,以OB为半径作⊙O.(1)判定直线AC是否是⊙O的切线,并说明理由;
角平分线交BC于O,以OB为半径作⊙O.(1)判定直线AC是否是⊙O的切线,并说明理由;
(2)连接AO交⊙O于点E,其延长线交⊙O于点D,![]() ,求
,求![]() 的值;
的值;
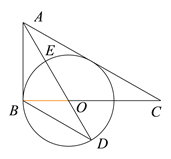
(3)在(2)的条件下,设![]() 的半径为3,求AC的长.
的半径为3,求AC的长.
参考答案:
【答案】(1)见解析;(2)![]()
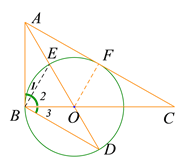
【解析】分析:(1)由于题目没有说明直线AC与⊙O有交点,所以过点O作OF⊥AC于点F,然后证明OB=OF即可;
(2)连接BE,先求证∠ABE=∠ODB,然后可知△ABE∽△ADB,所以![]() ,而tan∠D=
,而tan∠D=![]() ,于是得到结论;
,于是得到结论;
(3)设![]() 在
在![]() 和
和![]() 中根据
中根据![]() 列二元一次方程组求解即可.
列二元一次方程组求解即可.
详解:(1)AC是⊙O的切线
理由:![]()
![]() ,
,![]()
![]() ,
,
作![]() 于
于![]() ,
,
![]()
![]() 是
是![]() 的角平分线,
的角平分线,
![]() ,
,
![]() AC是⊙O的切线
AC是⊙O的切线
(2)连接![]() ,
,
![]()
![]() 是⊙O的直径,
是⊙O的直径,
![]()
![]() ,即
,即![]() .
.
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
又![]()
![]() (同角) ,
(同角) ,
![]()
![]() ∽
∽ ![]() ,
,
![]()
![]()
![]()
(3) 设![]()
在![]() 和
和![]() 中,由三角函数定义有:
中,由三角函数定义有:
![]()
得: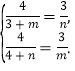
解之得:![]()
![]()
![]() 即
即![]() 的长为
的长为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】某文化用品商店用1 000元购进一批“晨光”套尺,很快销售一空;商店又用1 500元购进第二批该款套尺,购进时单价是第一批的
 倍,所购数量比第一批多100套.
倍,所购数量比第一批多100套.(1)求第一批套尺购进时单价是多少?
(2)若商店以每套4元的价格将这两批套尺全部售出,可以盈利多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知代数式M=(a+b+1)x3+(2a﹣b)x2+(a+2b)x﹣4是关于x的二次多项式.
(1)若方程3(a+b)y=ky﹣8的解是y=4,求k的值;
(2)当x=2时,代数式M的值为﹣34.当x=﹣2时,求代数式M的值.
-
科目: 来源: 题型:
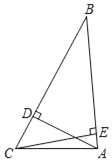
查看答案和解析>>【题目】在锐角△ABC中,AD与CE分别是边BC与AB的高,AB=12,BC=16,S△ABC=48,
求:(1)角B的度数;
(2)tanC的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
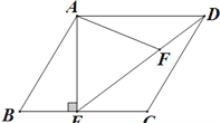
(1)求证:∠DAF=∠CDE;
(2)求证:△ADF∽△DEC;
(3)若AE=6,AD=8,AB=7,求AF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图本题图①,在等腰Rt
 中,
中,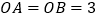 ,
,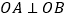 ,
,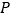 为线段
为线段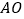 上一点,以
上一点,以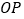 为半径作
为半径作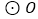 交
交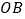 于点
于点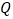 ,连接
,连接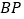 、
、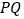 ,线段
,线段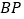 、
、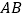 、
、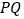 的中点分别为
的中点分别为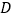 、
、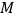 、
、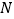 .
.(1)试探究
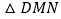 是什么特殊三角形?说明理由;
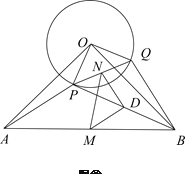
是什么特殊三角形?说明理由;(2)将
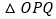 绕点
绕点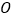 逆时针方向旋转到图②的位置,上述结论是否成立?并证明结论;
逆时针方向旋转到图②的位置,上述结论是否成立?并证明结论;(3)若
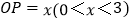 ,把
,把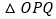 绕点
绕点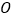 在平面内自由旋转,求
在平面内自由旋转,求 的面积y的最大值与最小值的差.
的面积y的最大值与最小值的差.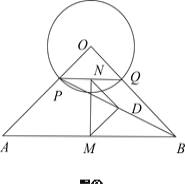
-
科目: 来源: 题型:
查看答案和解析>>【题目】若任意一个三位数t的百位数字为a,十位数字为b,个位数字为c,那么可将这个三位数表示为t=
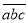 (a≠0),且满足t=100a+10b+c,我们把三位数各位上的数字的乘积叫做原数的积数,记为P(t).重新排列一个三位数各位上的数字,必可以得到一个最大的三位数和一个最小的三位数,此最大三位数与最小三位数之差叫做原数的差数,记为F(t),例如:264的积数P(264)=48,差数F(264)=642﹣246=396.
(a≠0),且满足t=100a+10b+c,我们把三位数各位上的数字的乘积叫做原数的积数,记为P(t).重新排列一个三位数各位上的数字,必可以得到一个最大的三位数和一个最小的三位数,此最大三位数与最小三位数之差叫做原数的差数,记为F(t),例如:264的积数P(264)=48,差数F(264)=642﹣246=396.(1)根据以上材料:F(258)= ;
(2)若一个三位数t=
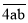 ,且P(t)=0,F(t)=135,求这个三位数.
,且P(t)=0,F(t)=135,求这个三位数.
相关试题

