【题目】如图,射线OA的方向是北偏东15°,射线OB的方向是北偏西40°,∠AOB=∠AOC,射线OD是OB的反向延长线.
(1)射线OC的方向是;
(2)求∠COD的度数;
(3)若射线OE平分∠COD,求∠AOE的度数.
参考答案:
【答案】
(1)北偏东70°
(2)解:∵∠AOB=55°,∠AOC=∠AOB,
∴∠BOC=110°.
∵射线OD是OB的反向延长线,
∴∠BOD=180°.
∴∠COD=180°-110°=70°
(3)解:∵∠COD=70°,OE平分∠COD,
∴∠COE=35°.
∵∠AOC=55°.
∴∠AOE=90°
【解析】解:(1)∵OB的方向是北偏西40°,OA的方向是北偏东15°,∴∠NOB=40°,∠NOA=15°,∴∠AOB=∠NOB+∠NOA=55°,
∵∠AOB=∠AOC,
∴∠AOC=55°,∴∠NOC=∠NOA+∠AOC=70°,
∴OC的方向是北偏东70°.
故答案为北偏东70°;(1)根据题意可知∠NOB=40°,∠NOA=15°,先求出∠AOB的度数,再根据∠AOB=∠AOC,得出∠AOC的度数,然后根据∠NOC=∠NOA+∠AOC,求出∠NOC的度数,就可得出OC的方向.
(2)先根据∠AOC=∠AOB,求出∠BOC的度数,再根据∠COD=180°-∠BOC的度数即可。
(3)根据∠COD=70°,OE平分∠COD,求出∠COE的度数,再根据∠AOE=∠COE+∠AOC,计算即可得出答案。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市为了增强学生体质,全面实施“学生饮用奶”营养工程.某品牌牛奶供应商提供了原味、草莓味、菠萝味、香橙味、核桃味五种口味的牛奶提供学生饮用.浠马中学为了了解学生对不同口味牛奶的喜好,对全校订购牛奶的学生进行了随机调查(每盒各种口味牛奶的体积相同),绘制了如图两张不完整的人数统计图:

(1)本次被调查的学生有 名;
(2)补全上面的条形统计图1,并计算出喜好“菠萝味”牛奶的学生人数在扇形统计图中所占圆心角的度数;
(3)该校共有1200名学生订购了该品牌的牛奶,牛奶供应商每天只为每名订购牛奶的学生配送一盒牛奶.要使学生每天都喝到自己喜好的口味的牛奶,牛奶供应商每天送往该校的牛奶中,草莓味要比原味多送多少盒?
-
科目: 来源: 题型:
查看答案和解析>>【题目】2019年10月7日统计,国庆假期重庆迎外地游客人数达到38590000次,38590000科学记数法表示为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(a,2019)与点A′(﹣2020,b)是关于原点O的对称点,则a+b的值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x,y为有理数,现规定一种运算“*”,满足x*y=xy+1(等式中xy表示x与y的积)
(1)求2*4的值;
(2)求(1*4)*(﹣2). -
科目: 来源: 题型:
查看答案和解析>>【题目】
(1)如图①,∠AOB=60°,OD平分∠BOC,OE平分∠AOC,则∠EOD=度;
(2)若∠AOB=90°,其它条件不变,则∠EOD=;
(3)若∠AOB=α,其它条件不变,则∠EOD= .
(4)类比应用:如图②,已知线段AB,C是线段AB上任一点,D、E分别是AC、CB的中点,试猜想DE与AB的数量关系为 , 并写出求解过程.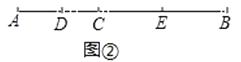
-
科目: 来源: 题型:
查看答案和解析>>【题目】用正方形硬纸板做三棱柱盒子,每个盒子由3个长方形侧面和2个正三角形底面组成,硬纸板以如图两种方法裁剪(裁剪后边角料不再利用).
A方法:剪6个侧面;
B方法:剪4个侧面和5个底面.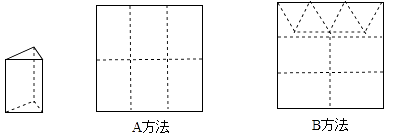
现有19张硬纸板,裁剪时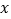 张用A方法,其余用B方法.
张用A方法,其余用B方法.
(1)分别求裁剪出的侧面和底面的个数(用含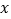 的式子表示);
的式子表示);
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
相关试题

