【题目】如图所示,在△ABC 中,AD 是 BC 边上的中线.
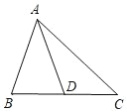
(1)画出与△ACD 关于点 D 成中心对称的三角形;
(2)找出与 AC 相等的线段;
(3)探索:△ABC 中,AB+AC 与中线 AD 之间的关系,并说明理由.
参考答案:
【答案】(1)详见解析;(2)A'B=AC;(3)AB+AC>2AD,理由详见解析.
【解析】
(1)作图;
(2)证明△ADC≌△A'DB,可知AC=A'B;
(3)根据三角形三边关系得:AB+BA'>AA',即AB+AC>AD+A'D,所以AB+AC>2AD.
(1)如图所示,延长 AD 至 A',使 AD=A'D,连接 A'B,则△A'DB 就是与△ACD 关于点 D 成中心对称的三角形;

(2)A'B=AC,
理由是:在△ADC 和△A'DB 中,
∵ ,
,
∴△ADC≌△A'DB(SAS),
∴AC=A'B;
(3)AB+AC>2AD;
理由:∵△ADC 与△A'DB 关于 D 点成中心对称,
∴AD=A'D,AC=A'B.
在△ABA'中,AB+BA'>AA', 即 AB+AC>AD+A'D.
∴AB+AC>2AD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠BAD=∠CBE=∠ACF,∠FDE=64°,∠DEF=43°,求△ABC各内角的度数.
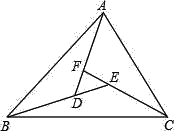
-
科目: 来源: 题型:
查看答案和解析>>【题目】“一带一路”战略为民营快递企业转变为跨境物流商提供了机遇.也让国民可以足不出户地买到世界各国的商品.小丝购买了一些物品,并了解到两家快递公司的收费方式.
甲公司:物品重量不超过1千克的,需付费20元,超过1千克的部分按每千克4元计价.
乙公司:按物品重量每千克7元计价,外加一份包装费10元.
设物品的重量为
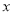 千克,甲、乙公司快递该物品的费用分别为
千克,甲、乙公司快递该物品的费用分别为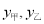 .
.
(1)写出
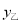 与
与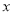 的函数表达式,并写出自变量
的函数表达式,并写出自变量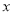 的取值范围;
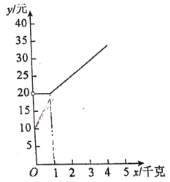
的取值范围;(2)图中给出了
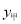 与
与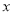 的函数图象,请在图中画出(1)中的函数图象;
的函数图象,请在图中画出(1)中的函数图象;(3)小丝需要快递的物品重量为4千克,如果想节省快递费用,结合图象指出,应选择的快递公司是________.
-
科目: 来源: 题型:
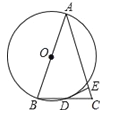
查看答案和解析>>【题目】已知AB是⊙O的直径,⊙O过BC的中点D,且DE垂直AC于E.
(1)求证:AB=AC;
(2)求证:DE是⊙O的切线;
(3)若AB=13,BC=10,求DE的长
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点.

(1)求该抛物线的解析式;
(2)求该抛物线的对称轴以及顶点坐标;
(3)设(1)中的抛物线上有一个动点P,当点P在该抛物线上滑动到什么位置时,满足S△PAB=8,并求出此时P点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,E,F为□ABCD 的对角线BD上的两点,且BE=DF.
求证:AE∥CF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
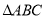 中,
中,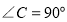 ,
,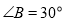 ,以
,以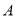 为圆心,任意长为半径画弧分别交
为圆心,任意长为半径画弧分别交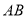 、
、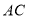 于点
于点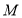 和
和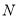 ,再分别以
,再分别以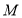 、
、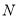 为圆心,大于
为圆心,大于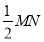 的长为半径画弧,两弧交于点
的长为半径画弧,两弧交于点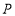 ,连结
,连结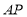 并延长交
并延长交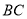 于点
于点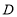 ,则下列说法中正确的个数是( )
,则下列说法中正确的个数是( )①
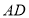 是
是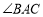 的平分线;②
的平分线;②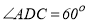 ;③点
;③点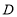 在
在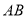 的垂直平分线上;④
的垂直平分线上;④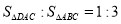
A.1B.2C.3D.4
相关试题

