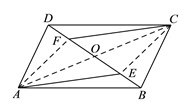
【题目】已知：如图，E，F为□ABCD 的对角线BD上的两点，且BE=DF．

求证：AE∥CF．

参考答案：

【答案】证明见解析

【解析】试题分析：连接AC交BD于点O，连接AF，CE，根据平行四边形的对角线互相平分可得OB＝OD，OA＝OC，再由BE=DF，可得OE＝OF，根据对角线互相平分的四边形是平行四边形可判定四边形AECF是平行四边形，所以AE∥CF．

试题解析：

证明：连接AC交BD于点O，

连接AF，CE.

∵四边形ABCD是平行四边形，

∴OB＝OD，OA＝OC．（平行四边形的对角线互相平分）

∵BE=DF，∴OB－BE＝OD－DF

即OE＝OF．

∴四边形AECF是平行四边形．（对角线互相平分的四边形是平行四边形）

∴AE∥CF．

关闭