搜索
【题目】如图，在
中，
，
，以
为圆心，任意长为半径画弧分别交
、
于点
和
，再分别以、为圆心，大于
的长为半径画弧，两弧交于点
，连结
并延长交
于点
，则下列说法中正确的个数是（ ）
①
是
的平分线；②
；③点在的垂直平分线上；④
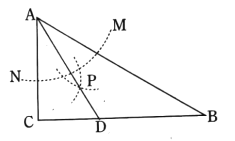
A.1B.2C.3D.4
参考答案：
【答案】D
【解析】
根据题干作图方式，可判断AD是∠CAB的角平分线，再结合∠B=30°，可推导得到△ABD是等腰三角形，根据这2个判定可推导题干中的结论.
题干中作图方法是构造角平分线，①正确；
∵∠B=30°，∠C=90°，AD是∠CAB的角平分线
∴∠CAD=∠DAB=30°
∴∠ADC=60°，②正确
∵∠DAB=∠B=30°
∴△ADB是等腰三角形
∴点D在AB的垂直平分线上，③正确
在Rt△CDA中，设CD=
，则AD=2
在△ADB中，DB=AD=2
∵
，
∴
，④正确
故选：D
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，在△ABC 中，AD 是 BC 边上的中线．
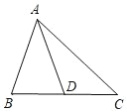
（1）画出与△ACD 关于点 D 成中心对称的三角形；
（2）找出与 AC 相等的线段；
（3）探索：△ABC 中，AB+AC 与中线 AD 之间的关系，并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线y=x2+bx+c与x轴交于A（-1，0），B（3，0）两点．
（1）求该抛物线的解析式；
（2）求该抛物线的对称轴以及顶点坐标；
（3）设（1）中的抛物线上有一个动点P，当点P在该抛物线上滑动到什么位置时，满足S△PAB=8，并求出此时P点的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图，E，F为□ABCD 的对角线BD上的两点，且BE=DF．
求证：AE∥CF．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某企业设计了一款工艺品，每件的成本是50元，为了合理定价，投放市场进行试销．据市场调查，销售单价是100元时，每天的销售量是50件，而销售单价每降低1元，每天就可多售出5件，但要求销售单价不得低于成本．
（1）求出每天的销售利润y（元）与销售单价x（元）之间的函数关系式；
（2）求出销售单价为多少元时，每天的销售利润最大？最大利润是多少？
（3）如果该企业要使每天的销售利润不低于4000元，且每天的总成本不超过7000元，那么销售单价应控制在什么范围内？（每天的总成本＝每件的成本×每天的销售量）
-
科目： 来源： 题型：
查看答案和解析>>【题目】某校积极推进“阳光体育”工程，本学期在九年级11个班中开展篮球单循环比赛（每个班与其它班分别进行一场比赛，每班需进行10场比赛）．比赛规则规定：每场比赛都要分出胜负，胜一场得3分，负一场得﹣1分．
（1）如果某班在所有的比赛中只得14分，那么该班胜负场数分别是多少？
（2）假设比赛结束后，甲班得分是乙班的3倍，甲班获胜的场数不超过5场，且甲班获胜的场数多于乙班，请你求出甲班、乙班各胜了几场．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线y＝－x2－2x＋3的图象与x轴交于A、B两点(点A在点B的左边)，与y轴交于点C，点D为抛物线的顶点．
(1)求点A、B、C的坐标；
(2)点M为线段AB上一点(点M不与点A、B重合)，过点M作x轴的垂线，与直线AC交于点E，与抛物线交于点P，过点P作PQ∥AB交抛物线于点Q，过点Q作QN⊥x轴于点N，若点P在点Q左边，当矩形PMNQ的周长最大时，求△AEM的面积；
(3)在(2)的条件下，当矩形PMNQ的周长最大时，连接DQ，过抛物线上一点F作
y轴的平行线，与直线AC交于点G(点G在点F的上方)．若，
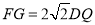
求点F的坐标．
相关试题
