【题目】已知AB是⊙O的直径,⊙O过BC的中点D,且DE垂直AC于E.
(1)求证:AB=AC;
(2)求证:DE是⊙O的切线;
(3)若AB=13,BC=10,求DE的长
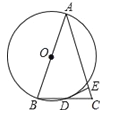
参考答案:
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】试题分析:(1)连结AD,如图,由圆周角定理得到∠ADB=90°,则AD⊥BC,加上BD=CD,即AD垂直平分BC,所以AB=AC;
(2)连结OD,如图,先证明OD为△ABC的中位线,根据三角形中位线性质得OD∥AC,而DE⊥AC,所以OD⊥DE,于是根据切线的判定定理可得DE是⊙O的切线;
(3)易得BD=DC=![]() BC=5,AC=AB=13,由勾股定理得到AD=12,再用面积法求出DE的长.
BC=5,AC=AB=13,由勾股定理得到AD=12,再用面积法求出DE的长.
试题解析:解:(1)连结AD,如图,∵AB为⊙O的直径,∴∠ADB=90°,∴AD⊥BC,∴D为BC的中点,∴BD=CD,∴AB=AC;

(2)连结OD,如图,∵OA=OB,DB=DC,∴OD为△ABC的中位线,∴OD∥AC,∵DE⊥AC,∴OD⊥DE,∴DE是⊙O的切线;
(3)BD=DC= ![]() BC=5,AC=AB=13,由勾股定理得:AD=12,在Rt△DAC中,
BC=5,AC=AB=13,由勾股定理得:AD=12,在Rt△DAC中, ![]() AD*DC=
AD*DC=![]() AC*DE,∴DE=
AC*DE,∴DE=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用工件槽(如图1)可以检测一种铁球的大小是否符合要求,已知工件槽的两个底角均为90°,尺寸如图(单位:cm).将形状规则的铁球放入槽内时,若同时具有图1所示的A、B、E三个接触点,该球的大小就符合要求.图2是过球心O及A、B、E三点的截面示意图,求这种铁球的直径.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠BAD=∠CBE=∠ACF,∠FDE=64°,∠DEF=43°,求△ABC各内角的度数.
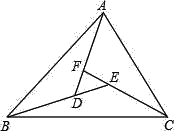
-
科目: 来源: 题型:
查看答案和解析>>【题目】“一带一路”战略为民营快递企业转变为跨境物流商提供了机遇.也让国民可以足不出户地买到世界各国的商品.小丝购买了一些物品,并了解到两家快递公司的收费方式.
甲公司:物品重量不超过1千克的,需付费20元,超过1千克的部分按每千克4元计价.
乙公司:按物品重量每千克7元计价,外加一份包装费10元.
设物品的重量为
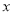 千克,甲、乙公司快递该物品的费用分别为
千克,甲、乙公司快递该物品的费用分别为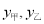 .
.
(1)写出
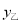 与
与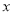 的函数表达式,并写出自变量
的函数表达式,并写出自变量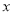 的取值范围;
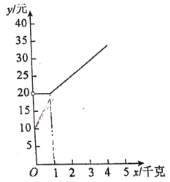
的取值范围;(2)图中给出了
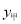 与
与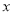 的函数图象,请在图中画出(1)中的函数图象;
的函数图象,请在图中画出(1)中的函数图象;(3)小丝需要快递的物品重量为4千克,如果想节省快递费用,结合图象指出,应选择的快递公司是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC 中,AD 是 BC 边上的中线.
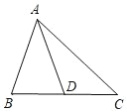
(1)画出与△ACD 关于点 D 成中心对称的三角形;
(2)找出与 AC 相等的线段;
(3)探索:△ABC 中,AB+AC 与中线 AD 之间的关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点.

(1)求该抛物线的解析式;
(2)求该抛物线的对称轴以及顶点坐标;
(3)设(1)中的抛物线上有一个动点P,当点P在该抛物线上滑动到什么位置时,满足S△PAB=8,并求出此时P点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,E,F为□ABCD 的对角线BD上的两点,且BE=DF.
求证:AE∥CF.

相关试题

