【题目】将下列证明过程补充完整:
已知:如图,点B.E分别在AC、DF上,AF分别交BD、CE于点M、N,∠1=∠2,∠A=∠F.
求证:∠C=∠D.

证明:因为∠1=∠2(已知).
又因为∠1=∠ANC(______),
所以______(等量代换).
所以______∥______(同位角相等,两直线平行).
所以∠ABD=∠C(______).
又因为∠A=∠F(已知),
所以______∥______(______).
所以______(两直线平行,内错角相等).
所以∠C=∠D(______).
参考答案:
【答案】见解析.
【解析】根据对顶角相等可知∠1=∠ANC,根据同位角相等,两直线平行,可知DB∥EC,再根据平行线的性质可知∠ABD=∠C,再根据平行线的性质以及判定即可得出答案.
证明:∵∠1=∠2(已知).
又∵∠1=∠ANC(对顶角相等),
∴∠2=∠ANC(等量代换).
∴DB∥EC(同位角相等,两直线平行).
∴∠ABD=∠C(两直线平行,同位角相等)
又∵∠A=∠F(已知),
∴DF∥AC(内错角相等,两直线平行),
∴∠D=∠ABD(两直线平行,内错角相等).
∴∠C=∠D(等量代换).
-
科目: 来源: 题型:
查看答案和解析>>【题目】去学校食堂就餐,经常会在一个买菜窗口前等待,经调查发现,同学的舒适度指数y与等时间x(分)之间满足反比例函数关系,如下表:
等待时间x
1
2
5
10
20
舒适度指数y
100
50
20
10
5
已知学生等待时间不超过30分钟
(1)求y与x的函数关系式,并写出自变量x的取值范围.
(2)若等待时间8分钟时,求舒适度的值;
(3)舒适度指数不低于10时,同学才会感到舒适.请说明,作为食堂的管理员,让每个在窗口买菜的同学最多等待多少时间? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2﹣(m+2)x+2m﹣1=0.
(1)求证:此方程有两个不相等的实数根;
(2)若抛物线y=x2﹣(m+2)x+2m﹣1=0与x轴有两个交点都在x轴正半轴上,求m的取值范围;
(3)填空:若x2﹣(m+2)x+2m﹣1=0的两根都大于1,则m的取值范围是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,⊙P经过y轴上一点C,与x轴分别相交于A、B两点,连接BP并延长分别交⊙P、y轴于点D、E,连接DC并延长交x轴于点F.若点F的坐标为(﹣1,0),点D的坐标为(1,6).
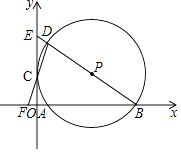
(1)求证:CD=CF;
(2)判断⊙P与y轴的位置关系,并说明理由;
(3)求直线BD的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,若∠A=15°,AB=BC=CD=DE=EF,则∠DEF等于__________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,∠BAC=90°,点D在射线BC上(与B、C两点不重合),以AD为边作正方形ADEF,使点E与点B在直线AD的异侧,射线BA与射线CF相交于点G.
(1)若点D在线段BC上,如图1.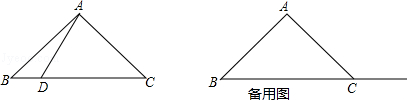
①依题意补全图1;
②判断BC与CG的数量关系与位置关系,并加以证明;
(2)若点D在线段BC的延长线上,且G为CF中点,连接GE,AB=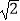 ,则GE的长为
,则GE的长为  ,并简述求GE长的思路.
,并简述求GE长的思路. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l:y=x﹣
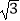 与x轴正半轴、y轴负半轴分别相交于A、C两点,抛物线y=
与x轴正半轴、y轴负半轴分别相交于A、C两点,抛物线y=  x2+bx+c经过点B(﹣1,0)和点C.
x2+bx+c经过点B(﹣1,0)和点C.
(1)填空:直接写出抛物线的解析式:;
(2)已知点Q是抛物线y= x2+bx+c在第四象限内的一个动点.
x2+bx+c在第四象限内的一个动点.
①如图,连接AQ、CQ,设点Q的横坐标为t,△AQC的面积为S,求S与t的函数关系式,并求出S的最大值;
②连接BQ交AC于点D,连接BC,以BD为直径作⊙I,分别交BC、AB于点E、F,连接EF,求线段EF的最小值,并直接写出此时Q点的坐标.
相关试题

