【题目】去学校食堂就餐,经常会在一个买菜窗口前等待,经调查发现,同学的舒适度指数y与等时间x(分)之间满足反比例函数关系,如下表:
等待时间x | 1 | 2 | 5 | 10 | 20 |
舒适度指数y | 100 | 50 | 20 | 10 | 5 |
已知学生等待时间不超过30分钟
(1)求y与x的函数关系式,并写出自变量x的取值范围.
(2)若等待时间8分钟时,求舒适度的值;
(3)舒适度指数不低于10时,同学才会感到舒适.请说明,作为食堂的管理员,让每个在窗口买菜的同学最多等待多少时间?
参考答案:
【答案】
(1)解:观察表格发现:1×100=2×50=5×20=…,
∴xy=100,
∴y= ![]() (0<x≤30)
(0<x≤30)
(2)解:当x=8时,舒适度y= ![]() =12.5
=12.5
(3)解:舒适度指数不低于10时,由图象y≥10时,0<x≤10
所以作为食堂的管理员,让每个在窗口买菜的同学最多等待10分钟
【解析】(1)观察表格发现:1×100=2×50=5×20,从而确定函数关系式y= ![]() ,y代表舒适度指数,x(分)代表等待时间.(2)是已知x=8,代入函数解析式求得y.(3)是已知y≥10,就可以得到关于x的不等式求的x的范围.
,y代表舒适度指数,x(分)代表等待时间.(2)是已知x=8,代入函数解析式求得y.(3)是已知y≥10,就可以得到关于x的不等式求的x的范围.
-
科目: 来源: 题型:
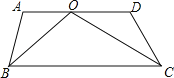
查看答案和解析>>【题目】如图所示,AD∥BC,BO,CO分别平分∠ABC,∠DCB,若∠A+∠D=n°,则∠BOC= 度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边三角形ABC中,已知点O是三个内角平分线的交点,OD∥AB,OE∥AC,则图中等腰三角形的个数是( )
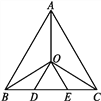
A. 4 B. 5 C. 6 D. 7
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,BC的垂直平分线EF交∠ABC的平分线BD于E,如果∠BAC=60°,∠ACE=24°,那么∠BCE的大小是( )

A. 24° B. 30° C. 32° D. 36°
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2﹣(m+2)x+2m﹣1=0.
(1)求证:此方程有两个不相等的实数根;
(2)若抛物线y=x2﹣(m+2)x+2m﹣1=0与x轴有两个交点都在x轴正半轴上,求m的取值范围;
(3)填空:若x2﹣(m+2)x+2m﹣1=0的两根都大于1,则m的取值范围是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,⊙P经过y轴上一点C,与x轴分别相交于A、B两点,连接BP并延长分别交⊙P、y轴于点D、E,连接DC并延长交x轴于点F.若点F的坐标为(﹣1,0),点D的坐标为(1,6).
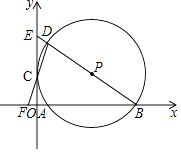
(1)求证:CD=CF;
(2)判断⊙P与y轴的位置关系,并说明理由;
(3)求直线BD的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】将下列证明过程补充完整:
已知:如图,点B.E分别在AC、DF上,AF分别交BD、CE于点M、N,∠1=∠2,∠A=∠F.
求证:∠C=∠D.

证明:因为∠1=∠2(已知).
又因为∠1=∠ANC(______),
所以______(等量代换).
所以______∥______(同位角相等,两直线平行).
所以∠ABD=∠C(______).
又因为∠A=∠F(已知),
所以______∥______(______).
所以______(两直线平行,内错角相等).
所以∠C=∠D(______).
相关试题

