搜索
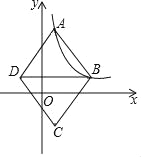
【题目】如图，在平面直角坐标系中，菱形ABCD的顶点A、B在反比例函数y=
（k＞0，x＞0）的图象上，横坐标分别为1，4，对角线BD∥x轴．若菱形ABCD的面积为
，则k的值为_____．
参考答案：
【答案】5
【解析】
连接AC分别交BD、x轴于点E、F．由菱形ABCD的面积为
，可求出AE的长，设点B的坐标为（4，y），则A点坐标为（1，y+
），由反比例函数图像上点的坐标特征可列方程求出y的值，从而可求出点B的坐标，进而可求出k的值.
连接AC分别交BD、x轴于点E、F．
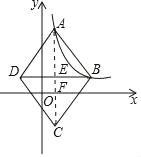
由已知，A、B横坐标分别为1，4，
∴BE=3，
∵四边形ABCD为菱形，AC、BD为对角线
∴S菱形ABCD=4×
AEBE=，
∴AE=，设点B的坐标为（4，y），则A点坐标为（1，y+）
∵点A、B同在y=
图象上
∴4y=1（y+）
∴y=
，
∴B点坐标为（4，）
∴k=5
故答案为5．
-
科目： 来源： 题型：
查看答案和解析>>【题目】若关于x的一元二次方程x2+（2k﹣1）x+k2=0的两根a、b满足a2﹣b2=0，双曲线
（x＞0）经过Rt△OAB斜边OB的中点D，与直角边AB交于C（如图），则S△OBC为（ ）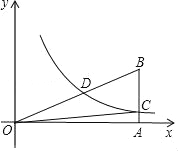
A. 3 B.
C. 6 D. 3或 -
科目： 来源： 题型：
查看答案和解析>>【题目】一辆汽车在某次行驶过程中，油箱中的剩余油量y（升）与行驶路程x（千米）之间是一次函数关系，其部分图象如图所示．
（1）求y关于x的函数关系式；（不需要写定义域）
（2）已知当油箱中的剩余油量为8升时，该汽车会开始提示加油，在此次行驶过程中，行驶了500千米时，司机发现离前方最近的加油站有30千米的路程，在开往该加油站的途中，汽车开始提示加油，这时离加油站的路程是多少千米？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点A是函数y=
图象上的一点，已知B（﹣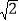
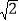，﹣），C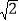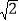（，）．试利用性质：“y=图象上的任意一点P都满足|PB﹣PC|=2”求解下面问题：作∠BAC的内角平分线AE，过B作AE的垂线交AE于F．当点A在函数y=图象上运动时，点F也总在一图形上运动，该图形为（ ）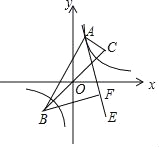
A. 圆 B. 双曲线 C. 抛物线 D. 直线
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线y=x+b交x轴于A点，交y轴于B点，与反比例函数y=
交于点D，作DC⊥x轴，DE⊥y轴，则ADBD的值为________．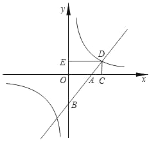
-
科目： 来源： 题型：
查看答案和解析>>【题目】某游泳馆每年夏季推出两种游泳付费方式，方式一：先购买会员证，每张会员证100元，只限本人当年使用，凭证游泳每次再付费5元；方式二：不购买会员证，每次游泳付费9元．
设小明计划今年夏季游泳次数为x（x为正整数）．
（I）根据题意，填写下表：
游泳次数
10
15
20
…
x
方式一的总费用（元）
150
175
______
…
______
方式二的总费用（元）
90
135
______
…
______
（Ⅱ）若小明计划今年夏季游泳的总费用为270元，选择哪种付费方式，他游泳的次数比较多？
（Ⅲ）当x>20时，小明选择哪种付费方式更合算？并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】关于一次函数y=﹣2x+3，下列结论正确的是（ ）
A. 图象过点（1，﹣1） B. 图象经过一、二、三象限
C. y随x的增大而增大 D. 当x＞
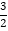时，y＜0
相关试题
