【题目】在△ABC中,如图∠BAC=90°,BD平分∠ABC,点E在BC上,DE∥AB,点F在BC上,连结AF,∠C=36°.
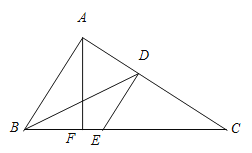
(1)求∠BDE的度数;
(2)若∠BAF∶∠CAF=2∶3,求证:AF⊥BC.
参考答案:
【答案】(1)27°;(2)见解析.
【解析】
(1)由∠BAC=90°和∠C=36°,可求得∠ABC,由BD平分∠ABC得∠ABD=![]() ∠ABC,
∠ABC,
再由DE∥AB,根据两直线平行,内错角相等可得∠BDE=∠ABD,问题得解;
(2)由∠BAF∶∠CAF=2∶3,可计算出∠CAF的度数,验证它与∠C的和等于90°即可.
(1)解:∵∠BAC=90°,∠C=36°,
∴∠ABC=54°,
∵BD平分∠ABC,
∴∠ABD=![]() ∠ABC=27°,
∠ABC=27°,
∵DE∥AB,
∴∠BDE=∠ABD=27°;
(2)证明:∵∠BAF∶∠CAF=2∶3,
∴∠CAF=![]() ∠BAC=
∠BAC=![]() ×90°=54°,
×90°=54°,
∵∠C=36°,
∴∠CAF+∠C=54°+36°=90°,
即∠AFC=90°,
∴AF⊥BC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线经过点A(﹣3,0)、B(0,3),C(1,0).
(1)求抛物线及直线AB的函数关系式;
(2)有两动点D、E同时从O出发,以每秒1个单位长度的相同的速度分别沿线段OA、OB向A、B做匀速运动,过D作PD⊥OA分别交抛物线和直线AB于P、Q,设运动时间为t(0<t<3).
①求线段PQ的长度的最大值;
②连接PE,当t为何值时,四边形DOEP是正方形;
③连接DE,在运动过程中,是否存在这样的t值,使PE=DE?若存在,请求出t的值;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC,则下列结论:①abc<0;②
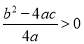 ;③ac﹣b+1=0;④OAOB=﹣
;③ac﹣b+1=0;④OAOB=﹣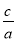 .其中正确结论的序号是_____.
.其中正确结论的序号是_____.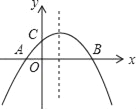
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程:
(1)
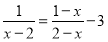 ;
;(2)
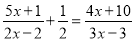 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】“安全教育平台”是中国教育学会为方便学长和学生参与安全知识活动、接受安全提醒的一种应用软件.某校为了了解家长和学生参与“防溺水教育”的情况,在本校学生中随机抽取部分学生作调查,把收集的数据分为以下4类情形:A.仅学生自己参与;B.家长和学生一起参与;
C.仅家长自己参与; D.家长和学生都未参与.

请根据图中提供的信息,解答下列问题:
(1)在这次抽样调查中,共调查了________名学生;
(2)补全条形统计图,并在扇形统计图中计算C类所对应扇形的圆心角的度数;
(3)根据抽样调查结果,估计该校2000名学生中“家长和学生都未参与”的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,过点A(2,0)的直线l与y轴交于点B,tan∠OAB=
 ,直线l上的点P位于y轴左侧,且到y轴的距离为1.
,直线l上的点P位于y轴左侧,且到y轴的距离为1.(1)求直线l的表达式;
(2)若反比例函数
 的图象经过点P,求m的值.
的图象经过点P,求m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的盒子里装有只有颜色不同的黑、白两种球共50个,小颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是试验中的一组统计数据:
摸到球的次数
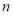
100
200
300
500
800
1000
3000
摸到白球的次数
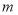
65
124
178
302
481
599
1803
摸到白球的概率
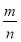
0.65
0.62
0.593
0.604
0.601
0.599
0.601
(1)请估计当
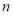 很大时,摸到白球的频率将会接近______;(精确到0.1);
很大时,摸到白球的频率将会接近______;(精确到0.1);(2)假如随机摸一次,摸到白球的概率P(白球)=______;
(3)试估算盒子里白色的球有多少个?
相关试题

