【题目】(1)观察思考
如图所示,线段AB上的点数与线段的总条数有如下关系:如果线段AB上有3个点,那么线段总条数为3;如果线段AB上有4个点,那么线段总条数为6;如果线段AB上有5个点,那么线段总条数为________.
![]() 3=2+1=
3=2+1=![]()
![]() 6=3+2+1=
6=3+2+1=![]()
![]()
(2)模型构建
如果线段上有m个点(包括线段的两个端点),那么共有________条线段.
(3)拓展应用
8位同学参加班上组织的象棋比赛,比赛采用单循环制(即每两位同学之间都要进行一场比赛),那么一共要进行多少场比赛?
请将这个问题转化为上述模型,并直接应用上述模型的结论解决问题.
参考答案:
【答案】(1)10 (2)![]() ;(3)见解析.
;(3)见解析.
(3)把8位同学看作线段上的8个点,每两位同学之间的一场比赛看作一条线段,线段上8个点所构成的线段条数就等于比赛的场数,因此一共要进行![]() =28(场)比赛.
=28(场)比赛.
【解析】(1)根据图形可以得出5个点的线段总数为1+2+3+4=10条,故得出结论;
(2)根据题意就可以得出m个点就有1+2+3+…+(m-1)=![]() 条线段;
条线段;
(3)将实际问题转化成(2)的模型,借助(2)的结论即可得出结论.
(1)根据题意可知线段AB上有5个点,那么线段总条数为1+2+3+4=10条,
故答案为:10;
(2)设线段上有m个点,该线段上共有线段x条,
则x=(m﹣1)+(m﹣2)+(m﹣3)+…+3+2+1,
∴倒序排列有x=1+2+3+…+(m﹣3)+(m﹣2)+(m﹣1),
∴2x=m(m﹣1),
∴x=![]() ,
,
故答案为:![]() ;
;
(3)把8位同学看作直线上的8个点,每两位同学之间的一场比赛看作为一条线段,
直线上8个点所构成的线段条数就等于比赛的场数,
因此一共要进行![]() =28场比赛,
=28场比赛,
答:一共要进行28场比赛.
-
科目: 来源: 题型:
查看答案和解析>>【题目】两个大小不同的等腰直角三角板如图①放置,图②是由它抽象出的几何图形,点B,C,E在同一条直线上,连接CD.求证:CD⊥BE.
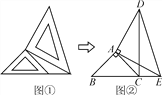
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,从教室B到图书馆A,总有少数同学不走人行横道而横穿草坪,他们这种做法是因为________,学校为制止这种现象,准备立一块警示牌,请你为该牌写一句话________________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】A、B、C、D是四个城市,现在要建造一个火力发电厂M,为了节省资金,应使输电线路最短,因此电厂到这四个城市距离之和最小,请你确定M的位置.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC=2∠C,∠BAC的平分线AD交BC于D,过B作BE⊥AD交AD于F,交AC于E.
(1)求证:△ABE为等腰三角形;
(2)已知AC=11,AB=6,求BD长.
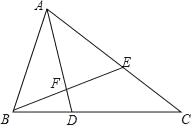
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列实数中是无理数的是( )
A.
B.tan30°
C.3.14
D.2﹣1 -
科目: 来源: 题型:
查看答案和解析>>【题目】在弹性限度内,弹簧挂上物体后会伸长,测得弹簧的长度
 与所挂物体的质量
与所挂物体的质量 之间有如下表关系:
之间有如下表关系:





…






…
下列说法不正确的是( )
A.
 随
随 的增大而增大 B. 所挂物体质量每增加
的增大而增大 B. 所挂物体质量每增加 弹簧长度增加
弹簧长度增加
C. 所挂物体为
 时,弹簧长度为
时,弹簧长度为 D. 不挂重物时弹簧的长度为
D. 不挂重物时弹簧的长度为
相关试题

