【题目】微信运动是由腾讯开发的一个类似计步数据库的公众账号,用户可以通过关注微信运动公众号查看自己每天行走的步数,同时也可以和其他用户进行运动量的![]() 或点赞.甲、乙两人开启了微信运动,沿湖边环形道上匀速跑步,已知乙的步距比甲的步距少
或点赞.甲、乙两人开启了微信运动,沿湖边环形道上匀速跑步,已知乙的步距比甲的步距少![]() (步距是指每一步的距离),两人各跑了
(步距是指每一步的距离),两人各跑了![]() 圈,跑
圈,跑![]() 圈前后的时刻和步数如下:
圈前后的时刻和步数如下:
出发时刻 | 出发时微信运动中显示的步数 | 结束时刻 | 结束时微信运动中显示的步数 | |
甲 |
|
|
|
|
乙 |
|
|
|
|
(1)求甲、乙的步距和环形道的周长;
(2)若每![]() 分钟甲比乙多跑
分钟甲比乙多跑![]() 步,求表中
步,求表中![]() 的值.
的值.
参考答案:
【答案】(1)甲的步距为![]() ,乙的步距为
,乙的步距为![]() ,环形道的周长为
,环形道的周长为![]() ;(2)
;(2)![]() 为
为![]() .
.
【解析】
(1)由于两人各跑3周后到达同一地点,可分别用甲和乙跑的总步数乘以各自的步距,列方程可得步距,从而求出环形道的周长;
(2)先由甲跑的总步数除以甲所用的时间,得出甲每分钟跑的步数,再根据每2分钟甲比乙多跑25步,得出乙每2分钟乙跑多少步,从而用乙的总步数除以乙每2分钟乙跑的步数,再乘以2,即可得乙所用的时间,从而可知a的值;
(1)设乙的步距为![]() ,由于乙的步距比甲的步距少
,由于乙的步距比甲的步距少![]() , 则甲的步距为
, 则甲的步距为![]() ,
,
根据表格列方程得:
![]() ,
,
![]() ,
,
![]() ,
,
![]() 环形道的周长为:
环形道的周长为:![]() .
.
故甲的步距为![]() ,乙的步距为
,乙的步距为![]() ,环形道的周长为
,环形道的周长为![]() .
.
(2)由表格知,甲![]() 分钟跑了步
分钟跑了步![]() ,则甲每分钟跑
,则甲每分钟跑![]() 步,
步,
![]() 每
每![]() 分钟甲比乙多跑
分钟甲比乙多跑![]() 步,
步,
![]() 每
每![]() 分钟甲比乙多跑
分钟甲比乙多跑![]() 步
步
![]() 每
每![]() 分钟乙跑
分钟乙跑![]() 步,
步,
![]()
![]() 分钟,
分钟,
![]()
![]() 为
为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD,点P是对角线AC上一点,连结BP,过P作PQ⊥BP,PQ交CD于Q,若AP=4
 ,CQ=10,则正方形ABCD的面积为 .
,CQ=10,则正方形ABCD的面积为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读下面的内容,再解决问题,例题:若m2+2mn+2n2﹣6n+9=0,求m和n的值.
解:∵m2+2mn+2n2﹣6n+9=0,
∴m2+2mn+n2+n2﹣6n+9=0,
∴(m+n)2+(n﹣3)2=0,
∴m+n=0,n﹣3=0,
∴m=﹣3,n=3
问题:
(1)若x2+2y2+2xy﹣4y+4=0,求
 x+y的值.
x+y的值.(2)已知a,b,c是△ABC的三边长,满足a2+b2=10a+8b﹣41,且c是△ABC中最长的边,求c的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,已知
中,已知 ,
, ,
, ,点
,点 在边
在边 上,
上, ,线段
,线段 绕点
绕点 顺时针旋转
顺时针旋转 度后(
度后( ),点
),点 旋转至点
旋转至点 ,如果点
,如果点 恰好落在
恰好落在 的边上,求
的边上,求 的面积.
的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一食堂需要购买盒子存放食物,盒子有A、B两种型号,单个盒子的容量和价格如表格所示.现有15升食物需要存放且要求每个盒子都要装满,由于A型号盒子正做促销活动:购买三个及三个以上可一次性每个返还现金1.5元,则该食堂购买盒子所需最少费用是__________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy内,点A在直线y=3x上(点A在第一象限),
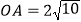 .
.(1)求点A的坐标;
(2)过点A作AB⊥x轴,垂足为点B,如果点E和点A都在反比例函数
 图像上(点E在第一象限),过点E作EF⊥y轴,垂足为点F,如果
图像上(点E在第一象限),过点E作EF⊥y轴,垂足为点F,如果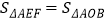 ,求点E的坐标.
,求点E的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】近年来,各地“广场舞”噪音干扰的问题备受关注,相关人员对本地区15﹣65岁年龄段的500名市民进行了随机调查,在调查过程中对“广场舞”噪音干扰的态度有以下五种:A:没影响;B:影响不大;C:有影响,建议做无声运动,D:影响很大,建议取缔;E:不关心这个问题,将调查结果绘统计整理并绘制成如下两幅不完整的统计图.

请根据以上信息解答下列问题:
(1)填空m= ,态度为C所对应的圆心角的度数为 ;
(2)补全条形统计图;
(3)若全区15﹣65岁年龄段有20万人,估计该地区对“广场舞”噪音干扰的态度为B的市民人数;
(4)若在这次调查的市民中,从态度为A的市民中抽取一人的年龄恰好在年龄段15﹣35岁的概率是多少?
相关试题

