【题目】如图,![]() 中
中![]() °,
°,![]() 垂直平分
垂直平分![]() ,
,![]() 垂直平分
垂直平分![]() ,则
,则![]() 的度数为( )
的度数为( )
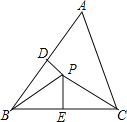
A.124°B.112°C.108°D.118°
参考答案:
【答案】B
【解析】
连接PA,根据线段垂直平分线上的点到线段两端点的距离相等可得PA=PB=PC,再根据等边对等角的性质可得∠PBA=∠PAB,∠PCA=∠PAC,然后利用三角形的内角和定理求出∠PBC+∠PCB的度数,再根据三角形的内角和等于180°进行计算即可求解.
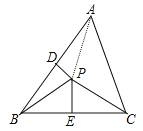
解:如图,连接PA,
∵PD垂直平分AB,PE垂直平分BC,
∴PA=PB,PB=PC,
∴PA=PB=PC,
∴∠PBA=∠PAB,∠PCA=∠PAC,
∵∠A=56°,
∴∠PBA+∠PCA=∠PAB+∠PAC=∠A=56°,
在△ABC中,∠PBC+∠PCB=180°∠A(∠PBA+∠PCA)=180°56°56°=68°,
在△PBC中,∠BPC=180°(∠PBC+∠PCB)=180°68°=112°.
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,AB是⊙O的一条弦,OD⊥AB,垂足为C,交⊙O于点D,点E在⊙O上.
(1)若∠AOD=52°,求∠DEB的度数;
(2)若OC=3,OA=5,求AB的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程x2+(2m﹣1)x+m2=0有实数根.
(1)求m的取值范围;
(2)若两根为x1、x2且x12+x22=7,求m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,点O是边BC的中点,连接AO并延长,交DC延长线于点E,连接AC,BE.
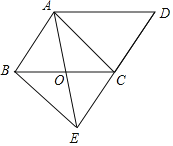
(1)求证:四边形ABEC是平行四边形;
(2)当∠D=50°,∠AOC=100°时,判断四边形ABEC的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为宣传节约用水,小强随机调查了某小区部分家庭3月份的用水情况,并将收集的数据整理成如下统计图.
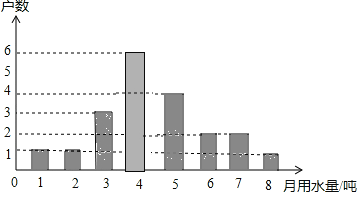
(1)小明一共调查了多少户家庭?
(2)求所调查家庭3月份用水量的众数、中位数和平均数;
(3)若该小区有800户居民,请你估计这个小区3月份的总用水量是多少吨?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,下列图形都是由面积为1的正方形按一定的规律组成,其中,图1中面积为1的正方形有9个,图2中面积为1的正方形有14个,
 ,按此规律,图12中面积为1的正方形的个数为
,按此规律,图12中面积为1的正方形的个数为

A.64B.60C.54D.50
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形
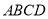 中,
中,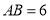 ,点
,点 在边
在边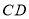 上,且
上,且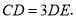 将
将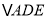 沿
沿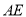 对折至
对折至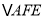 ,延长
,延长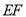 交边
交边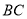 于点
于点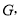 连结
连结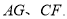 下列结论:①
下列结论:①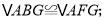 ②
②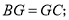 ③
③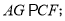 ④
④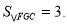
其中正确结论的个数是 ( )
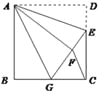
A.1B.2C.3D.4
相关试题

