搜索
【题目】如图所示，在平面直角坐标系中，已知
，
，
．
（1）在图中画出
，的面积是_____________；
（2）若点
与点
关于
轴对称，则点的坐标为_____________；
（3）已知
为轴上一点，若
的面积为
，求点的坐标．
参考答案：
【答案】（1）4；（2）
；（3）
或
【解析】
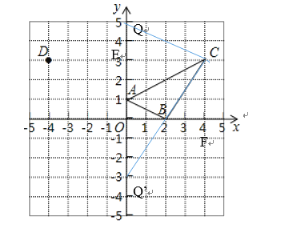
（1）根据指标坐标系中点的位置画出△ABC，作C垂直于y轴直线垂足为E, 作C垂直于x轴直线垂足为F,△ABC的面积等于矩形CEOF减去△CEA，△ABO,△BCF即可.
（2）根据对称轴的性质求出D坐标即可；
（3）△ACQ的高是CE为4，根据面积公式求出AQ，注意Q点为两组坐标.
解：（1）如图所示：S△ABC=S矩形CEOF-S△ABO-S△CEA-S△BCF
= 
；
故答案为：
；
（2）点
与点
关于
轴对称，则点的坐标为：；
故答案为：；
（3）
为
轴上一点，
的面积为
，
，
故
点坐标为：或．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，平面直角坐标系中，
，
为
轴正半轴上一点，连接
，在第一象限作
，
，过点
作直线
轴于
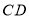，直线
与直线
交于点
，且
，则直线
解析式为____________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知，在Rt△ABC中，∠C=90°，AC=15，BC=8，D为AB的中点，E点在边AC上，将△BDE沿DE折叠得到△B1DE，若△B1DE与△ADE重叠部分面积为△ADE面积的一半，则CE=_____________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点P为x轴正半轴上的一个点，过点P作x轴的垂线，交函数
的图象于点A，交函数
的图象于点B，过点B作x轴的平行线，交于点C，边接AC．（1）当点P的坐标为（1，0）时，求△ABC的面积；
（2）当点P的坐标为（1，0）时，在y轴上是否存在一点Q，使A、O、Q三点为顶点的三角形△QAO为等腰三角形？若存在，请直接写出Q点的坐标；若不存在，说明理由．
（3）请你连接OA和OC．当点P的坐标为（t，0）时，△OAC的面积是否随t的值的变化而变化？请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】甲、乙两人相约周末登花果山，甲、乙两人距地面的高度y（米）与登山时间x（分）之间的函数图象如图所示，根据图象所提供的信息解答下列问题：
（1）甲登山上升的速度是每分钟 米，乙在A地时距地面的高度b为 米．
（2）若乙提速后，乙的登山上升速度是甲登山上升速度的3倍，请求出乙登山全程中，距地面的高度y（米）与登山时间x（分）之间的函数关系式．
（3）登山多长时间时，甲、乙两人距地面的高度差为50米？
-
科目： 来源： 题型：
查看答案和解析>>【题目】某校组织一项公益知识竞赛，比赛规定：每个班级由2名男生、2名女生及1名班主任老师组成代表队．但参赛时，每班只能有3名队员上场参赛，班主任老师必须参加，另外2名队员分别在2名男生和2名女生中各随机抽出1名．初三（1）班由甲、乙2名男生和丙、丁2名女生及1名班主任组成了代表队，求恰好抽到由男生甲、女生丙和这位班主任一起上场参赛的概率．（请用“画树状图”或“列表”或“列举”等方法给出分析过程）
-
科目： 来源： 题型：
查看答案和解析>>【题目】某学校为调查学生的兴趣爱好，抽查了部分学生，并制作了如下表格与条形统计图：
频数
频率
体育
40
0.4
科技
25
a
艺术
b
0.15
其它
20
0.2
请根据上图完成下面题目：
（1）总人数为 人，a= ，b= ．
（2）请你补全条形统计图．
（3）若全校有600人，请你估算一下全校喜欢艺术类学生的人数有多少？
相关试题
