【题目】如图,点P为x轴正半轴上的一个点,过点P作x轴的垂线,交函数![]() 的图象于点A,交函数
的图象于点A,交函数![]() 的图象于点B,过点B作x轴的平行线,交
的图象于点B,过点B作x轴的平行线,交![]() 于点C,边接AC.
于点C,边接AC.
(1)当点P的坐标为(1,0)时,求△ABC的面积;
(2)当点P的坐标为(1,0)时,在y轴上是否存在一点Q,使A、O、Q三点为顶点的三角形△QAO为等腰三角形?若存在,请直接写出Q点的坐标;若不存在,说明理由.
(3)请你连接OA和OC.当点P的坐标为(t,0)时,△OAC的面积是否随t的值的变化而变化?请说明理由.

参考答案:
【答案】(1)![]() ;(2)则Q的坐标为(0,﹣
;(2)则Q的坐标为(0,﹣![]() ),(0,
),(0,![]() ),(0,2)或(0,1);
),(0,2)或(0,1);
(3)见解析.
【解析】
(1)根据P点坐标先求出A,B两点坐标,然后求出C点坐标,得到AB=3,BC=![]() ,再利用三角形面积公式求解即可;
,再利用三角形面积公式求解即可;
(2)如图①,先求得OA=![]() ,再分OA=OQ,AQ=AO,QO=QA三种情况,分别求出Q点坐标即可;
,再分OA=OQ,AQ=AO,QO=QA三种情况,分别求出Q点坐标即可;
(3)如图②过点C作CE⊥x轴于点E,CD⊥y轴于点D,因为点P的坐标为(t,0),所以点A的坐标为(t,![]() ),点B(t,
),点B(t,![]() ),点C(
),点C(![]() ,
,![]() ),由图②可知S△OAC=S矩形CDOE+S梯形APEC﹣S△OCD﹣S△OAP,进而可得到关于t的方程,然后解方程即可.
),由图②可知S△OAC=S矩形CDOE+S梯形APEC﹣S△OCD﹣S△OAP,进而可得到关于t的方程,然后解方程即可.
解:(1)当点P的坐标为(1,0)时,点A、B的横坐标为1,
∵点A在反比例函数y=![]() 上,点B在反比例函数y=
上,点B在反比例函数y=![]() 上,
上,
∴点A(1,1),点B(1,4),
∵BC∥x轴,
∴点C的纵坐标为4,
又∵点C在y=![]() 上,
上,
∴点C的坐标为(![]() ,4),
,4),
∴AB=3,BC=![]() ,
,
∴S△ABC=![]() ×BC×AB=
×BC×AB=![]() ;
;
(2)如图①所示:OA=![]() =
=![]() ,
,
①若OA=OQ,点Q位于Q1或Q2位置,此时Q1(0,﹣![]() ),Q2(0,
),Q2(0,![]() );
);
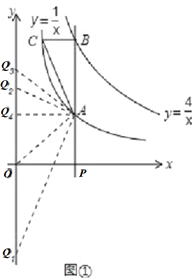
②若AQ=AO,点Q位于Q3位置,此时Q3(0,2);
③若QO=QA,点Q位于Q4位置,此时Q4(0,1);
则Q的坐标为(0,﹣![]() ),(0,
),(0,![]() ),(0,2)或(0,1);
),(0,2)或(0,1);
(3)过点C作CE⊥x轴于点E,CD⊥y轴于点D,如图②所示:
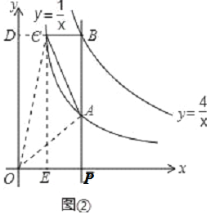
∵点P的坐标为(t,0),
∴点A的坐标为(t,![]() ),点B(t,
),点B(t,![]() ),点C(
),点C(![]() ,
,![]() ),
),
∴S△OAC=S矩形CDOE+S梯形APEC﹣S△OCD﹣S△OAP=1+![]() (
(![]() +
+![]() )×(t﹣
)×(t﹣![]() )﹣
)﹣![]() ﹣
﹣![]() =
=![]() ;
;
故△OAC的面积不随t的值的变化而变化.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,直线l:y=
 x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=
x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y= x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
x2+bx+c经过点B,与直线l的另一个交点为C(4,n).(1)求n的值和抛物线的解析式;
(2)点D在抛物线上,DE∥y轴交直线l于点E,点F在直线l上,且四边形DFEG为矩形(如图2),设点D的横坐标为t(0<t<4),矩形DFEG的周长为p,求p与t的函数关系式以及p的最大值;
(3)将△AOB绕平面内某点M旋转90°或180°,得到△A1O1B1,点A、O、B的对应点分别是点A1、O1、B1.若△A1O1B1的两个顶点恰好落在抛物线上,那么我们就称这样的点为“落点”,请直接写出“落点”的个数和旋转180°时点A1的横坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,
 ,
, 为
为 轴正半轴上一点,连接
轴正半轴上一点,连接 ,在第一象限作
,在第一象限作 ,
, ,过点
,过点 作直线
作直线 轴于
轴于 ,直线
,直线 与直线
与直线 交于点
交于点 ,且
,且 ,则直线
,则直线 解析式为____________.
解析式为____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,在Rt△ABC中,∠C=90°,AC=15,BC=8,D为AB的中点,E点在边AC上,将△BDE沿DE折叠得到△B1DE,若△B1DE与△ADE重叠部分面积为△ADE面积的一半,则CE=_____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在平面直角坐标系中,已知
 ,
, ,
, .
.
(1)在图中画出
 ,
,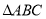 的面积是_____________;
的面积是_____________;(2)若点
 与点
与点 关于
关于 轴对称,则点
轴对称,则点 的坐标为_____________;
的坐标为_____________;(3)已知
 为
为 轴上一点,若
轴上一点,若 的面积为
的面积为 ,求点
,求点 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人相约周末登花果山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山上升的速度是每分钟 米,乙在A地时距地面的高度b为 米.
(2)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式.
(3)登山多长时间时,甲、乙两人距地面的高度差为50米?

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校组织一项公益知识竞赛,比赛规定:每个班级由2名男生、2名女生及1名班主任老师组成代表队.但参赛时,每班只能有3名队员上场参赛,班主任老师必须参加,另外2名队员分别在2名男生和2名女生中各随机抽出1名.初三(1)班由甲、乙2名男生和丙、丁2名女生及1名班主任组成了代表队,求恰好抽到由男生甲、女生丙和这位班主任一起上场参赛的概率.(请用“画树状图”或“列表”或“列举”等方法给出分析过程)
相关试题

