【题目】如图,二次函数 ![]() 的图象与x轴交于点 A,B,与y轴交于点C.点P是该函数图象上的动点,且位于第一象限,设点P的横坐标为x.
的图象与x轴交于点 A,B,与y轴交于点C.点P是该函数图象上的动点,且位于第一象限,设点P的横坐标为x.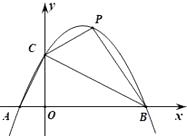
(1)写出线段AC,BC的长度:AC= , BC=;
(2)记△BCP的面积为S,求S关于x的函数表达式;
(3)过点P作PH⊥BC,垂足为H,连结AH,AP,设AP与BC交于点K,探究:是否存在四边形ACPH为平行四边形?若存在,请求出 ![]() 的值;若不存在,请说明理由,并求出
的值;若不存在,请说明理由,并求出 ![]() 的最大值.
的最大值.
参考答案:
【答案】
(1)解:AC= ![]() ,BC=
,BC= ![]()
(2)解:设P(x, ![]() ),则有
),则有 ![]()
= ![]() =
= ![]()
(3)解:过点P作PH⊥BC于H,
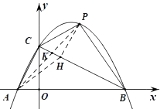
∵ ![]() ,
,
∴△ABC为直角三角形,即AC⊥BC;∴AC∥PH,
要使四边形ACPH为平行四边形,只需满足PH=AC= ![]() ,
,
∴ ![]() =5,而
=5,而 ![]() =
= ![]() =
= ![]() ,
,
所以不存在四边形ACPH为平行四边形
由△AKC∽△PHK,
∴ ![]() =
= ![]() (当x=2时,取到最大值)
(当x=2时,取到最大值)
【解析】(1)根据二次函数解析式写出A、B、C点的坐标,利用勾股定理即可得出AC、BC的长。
(2)求三角形的面积常用割补法,题解过程中,利用坐标系先进行补,在分割减法,即S = S Δ O C P + S Δ O B P S Δ O B C
(3)首先判定四边形是否存在,根据(2)求出PH长,和(1)中AC的长,得出对应边无法相等,所以四边形不存在,根据相似求出![]() 的值。
的值。
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列因式分解的过程:
①x2-xy+4x-4y=(x2-xy)+(4x-4y)=x(x-y)+4(x-y)=(x-y)(x+4).
②a2-b2-c2+2bc=a2-(b2+c2-2bc)=a2-(b-c)2=(a+b-c)(a-b+c).
第①题分组后能直接提公因式,第②题分组后能直接运用公式,仿照上述分解因式的方法,把下列各式分解因式:
(1)ad-ac-bc+bd;
(2)x2-6x+9-y2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两位同学利用灯光下的影子来测量一路灯A的高度,如图,当甲走到点C处时,乙测得甲直立身高CD与其影子长CE正好相等,接着甲沿BC方向继续向前走,走到点E处时,甲直立身高EF的影子恰好是线段EG,并测得EG=2.5m.已知甲直立时的身高为1.75m,求路灯的高AB的长.(结果精确到0.1m)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上有 A、B 两点,所表示的有理数分别为 a、b,已知 AB=12,原点 O 是线段AB 上的一点,且 OA=2OB.

(1)求a,b;
(2)若动点 P,Q 分别从 A,B 同时出发,向右运动,点 P 的速度为每秒 2 个单位长度,点 Q 的速度为每秒 1 个单位长度,设运动时间为 t 秒,当点 P 与点 Q 重合时,P,Q 两点停止运动.
①当 t 为何值时,2OPOQ=4;
②当点 P 到达点 O 时,动点 M 从点 O 出发,以每秒 3 个单位长度的速度也向右运动,当点 M 追上点 Q 后立即返回,以同样的速度向点 P 运动,遇到点 P 后再立即返回,以同样的速度向点 Q 运动,如此往返,直到点 P,Q 停止时,点 M 也停止运动,求在此过程中点 M 行驶的总路程,并直接写出点 M 最后位置在数轴上所对应的有理数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,
 ,连结AC,过点C作直线l∥AB,点P是直线l上的一个动点,直线PA与⊙O交于另一点D,连结CD,设直线PB与直线AC交于点E.
,连结AC,过点C作直线l∥AB,点P是直线l上的一个动点,直线PA与⊙O交于另一点D,连结CD,设直线PB与直线AC交于点E.
(1)求∠BAC的度数;
(2)当点D在AB上方,且CD⊥BP时,求证:PC=AC;
(3)在点P的运动过程中
①当点A在线段PB的中垂线上或点B在线段PA的中垂线上时,求出所有满足条件的∠ACD的度数;
②设⊙O的半径为6,点E到直线l的距离为3,连结BD, DE,直接写出△BDE的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校七年级全体学生在5名教师的带领下去公园秋游,公园的门票为每人30元.现有两种优惠方案,甲方案:带队老师免费,学生按8折收费;乙方案:师生都按7.5折收费.
(1)若有n名学生,用含n的代数式表示两种优惠方案各需多少元?
(2)当n=70时,采用哪种方案更优惠?
(3)当n=100时,采用哪种方案更优惠?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知,点A(0,0)、B(4
 ,0)、C(0,4),在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1 , 第2个△B1A2B2 , 第3个△B2A3B3 , …则第2017个等边三角形的边长等于( )
,0)、C(0,4),在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1 , 第2个△B1A2B2 , 第3个△B2A3B3 , …则第2017个等边三角形的边长等于( ) 
A.
B.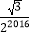
C.
D.
相关试题

