【题目】(1)已知两点A(3,m),B(2m,4),且A和B到x轴距离相等,求B点坐标.
(2)点A在第四象限,当m为何值时,点A(m+2,3m5)到x轴的距离是它到y轴距离的一半.
参考答案:
【答案】(1)(8,4)或(8,4);(2)![]() .
.
【解析】
(1)因为点A(3,m),B(2m,4),且A和B到x轴距离相等,所以,纵坐标相等或互为相反数;(2)因为,点A在第四象限,当m为何值时,点A(m+2,3m5)到x轴的距离是它到y轴距离的一半.所以,m+2>0,3m-5<0;2(5-3m)=m+2.
解:(1)因为点A(3,m),B(2m,4),且A和B到x轴距离相等,
所以,纵坐标相等或互为相反数,即m=4,2m=8,或m=-4,2m=-8
所以,B(8,4)或(8,4);
(2)
因为,点A在第四象限
所以,m+2>0 ,3m-5<0
所以,m+2是到y轴的距离
5-3m是到x轴的距离
所以,依题意得:2(5-3m)=m+2
10-6m=m+2
m=![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,某拦水大坝的横断面为梯形ABCD,AE、DF为梯形的高,其中迎水坡AB的坡角α=45°,坡长AB=
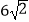 米,背水坡CD的坡度i=1:
米,背水坡CD的坡度i=1: 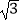 (i为DF与FC的比值),则背水坡CD的坡长为米.
(i为DF与FC的比值),则背水坡CD的坡长为米.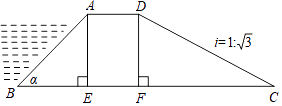
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,将射线Ox按逆时针方向旋转β,得到的射线Oy,如果P为射线Oy上的一点,且OP=a,那么我们规定用(a,β)表示点P在平面内的位置,并记为(a,β).例如,图②中,如果OM=8,∠xOM=110°,那么点M在平面内的位置记为M(8,110°),根据图形,解答下列问题:
(1)如图③,如果点N在平面内的位置记为N(6,30°),那么ON=__ __,∠xON= .
(2)如果点A,B在平面内的位置分别记为A(5,30°),B(12,120°),求A,B两点之间的距离.

-
科目: 来源: 题型:
查看答案和解析>>【题目】第1个等式:1-
 =
= ×
×
第2个等式:(1-
 )(1-
)(1- )=
)= ×
×
第3个等式:(1-
 )(1-
)(1- )(1-
)(1- )=
)= ×
×
第4个等式:(1-
 )(1-
)(1- )(1-
)(1- )(1-
)(1- )=
)= ×
×
第5个等式:(1-
 )(1-
)(1- )(1-
)(1- )(1-
)(1- )(1-
)(1- )=
)= ×
×
······
(1) 写出第6个等式;
(2) 写出第n个等式(用含n的等式表示),并予以证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】好学小东同学,在学习多项式乘以多项式时发现:(
 x+4)(2x+5)(3x-6)的结果是一个多项式,并且最高次项为:
x+4)(2x+5)(3x-6)的结果是一个多项式,并且最高次项为: x2x3x=3x3,常数项为:4×5×(-6)=-120,那么一次项是多少呢?要解决这个问题,就是要确定该一次项的系数.根据尝试和总结他发现:一次项系数就是:
x2x3x=3x3,常数项为:4×5×(-6)=-120,那么一次项是多少呢?要解决这个问题,就是要确定该一次项的系数.根据尝试和总结他发现:一次项系数就是: ×5×(-6)+2×(-6)×4+3×4×5=-3,即一次项为-3x.
×5×(-6)+2×(-6)×4+3×4×5=-3,即一次项为-3x.请你认真领会小东同学解决问题的思路,方法,仔细分析上面等式的结构特征.结合自己对多项式乘法法则的理解,解决以下问题.
(1)计算(x+2)(3x+1)(5x-3)所得多项式的一次项系数为_____.
(2)(
 x+6)(2x+3)(5x-4)所得多项式的二次项系数为_______.
x+6)(2x+3)(5x-4)所得多项式的二次项系数为_______.(3)若计算(x2+x+1)(x2-3x+a)(2x-1)所得多项式不含一次项,求a的值;
(4)若(x+1)2021=a0x2021+a1x2020+a2x2019+···+a2020x+a2021,则a2020=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,已知AB=AC,AB的垂直平分线交AB于点N,交AC于点M,连接MB.
(1)若∠ABC=70°,则∠NMA的度数是 度.
(2)若AB=8cm,△MBC的周长是14cm.
①求BC的长度;
②若点P为直线MN上一点,请你直接写出△PBC周长的最小值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(8分)如图所示,在四边形ABCD中,AB=2
 ,BC=2,CD=1,AD=5,且∠C=90°,求四边形ABCD的面积.
,BC=2,CD=1,AD=5,且∠C=90°,求四边形ABCD的面积.
相关试题

