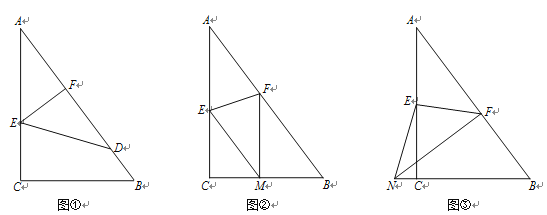
【题目】如图,已知一个直角三角形纸片ACB,其中∠ACB=90°,AC=4,BC=3,E、F分别是AC、AB边上点,连接EF,将纸片ACB的一角沿EF折叠.
(1)如图①,若折叠后点A落在AB边上的点D处,且使S四边形ECBF=3S△AEF,则AE= ;
(2)如图②,若折叠后点A落在BC边上的点M处,且使MF∥CA.求AE的长;
(3)如图③,若折叠后点A落在BC延长线上的点N处,且使NF⊥AB.求AE的长.
参考答案:
【答案】(1)AE=![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】(1)AE=![]() ;………………2分
;………………2分
(2)如图②,设AE=x,则CE=4-x.
∵∠ACB=90°,AC=4,BC=3,∴AB=5.
由折叠可知:AE=EM=x,AF=MF,∠AFE=∠MFE,
∵MF∥AC,∴∠AEF=∠MFE.∴∠AEF=∠AFE.
∴AE=AF.∴AE=EM=MF=AF,
∴四边形AEMF为菱形.………………4分
∴EM∥AB.∴△CME∽△CBA.………………5分
∴![]() =
=![]() ,即
,即![]() =
=![]() ,解得x=
,解得x=![]() ,即AE=
,即AE=![]() ………………6分
………………6分
(3)如图③,设AE=y,则CE=4-y.
由折叠可知:AE=EN=y,AF=NF,
∵NF⊥AB,∴∠NFB=90°.∵∠ACB=90°,∴∠NFB=∠ACB.
 且∠NBF=∠ABC,∴△NBF ∽△ABC.………………7分
且∠NBF=∠ABC,∴△NBF ∽△ABC.………………7分
∴![]() =
=![]() =
=![]() .即BF=
.即BF=![]() NF=
NF=![]() AF.由BF+ AF=AB=5,
AF.由BF+ AF=AB=5,
解得:BF=![]() ,NF=
,NF=![]() ,………………8分
,………………8分
∴BN=![]() ,CN=BN-BC=
,CN=BN-BC=![]() -3=
-3=![]() .………………9分
.………………9分
![]() 在Rt△CEN中,由CN2+CE2=EN2,∴(
在Rt△CEN中,由CN2+CE2=EN2,∴(![]() )2+(4-y)2=y2,
)2+(4-y)2=y2,
解得:y=![]() ,即AE=
,即AE=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
(1)求证:CE=AD;
(2)当D在AB中点时.
①求证:四边形BECD是菱形;
②当∠A为多少度时,四边形BECD是正方形?说明理由.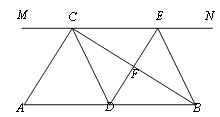
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线y=﹣5x+10一定通过下列点中的( )
A. (0,2)B. (2,0)C. (1,﹣5)D. (﹣1,5)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在平面直角坐标系中,半径均为1个单位长度的半圆O1、O2、O3,…组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒
 个单位长度,则第2015秒时,点P的坐标是( )
个单位长度,则第2015秒时,点P的坐标是( )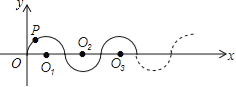
A. (2014,0) B. (2015,﹣1) C. (2015,1) D. (2016,0)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,以AC为直径的⊙O与边AB、BC分别交于点D、E.过E的直线与⊙O相切,与AC的延长线交于点G,与AB交于点F.
(1)求证:△BDE为等腰三角形;
(2)求证:GF⊥AB;
(3)若⊙O半径为3,DF=1,求CG的长.
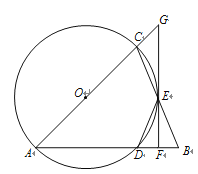
-
科目: 来源: 题型:
查看答案和解析>>【题目】若点P(a,b)在第三象限,则点Q(﹣a,b)一定在( )
A. 第一象限B. 第二象限C. 第三象限D. 第四象限
-
科目: 来源: 题型:
查看答案和解析>>【题目】若点A(x1,y1)和B(x2,y2)是直线y=﹣3x+4上的两点,且x1>x2,则y1与y2的大小关系是( )
A. y1<y2B. y1=y2C. y1>y2D. 不能确定
相关试题

