【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC,点D刚好落在AB边上. 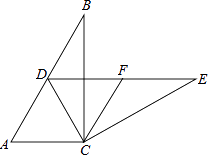
(1)求n的值;
(2)若F是DE的中点,判断四边形ACFD的形状,并说明理由.
参考答案:
【答案】
(1)解:∵在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC,
∴AC=DC,∠A=60°,
∴△ADC是等边三角形,
∴∠ACD=60°,
∴n的值是60
(2)解:四边形ACFD是菱形;
理由:∵∠DCE=∠ACB=90°,F是DE的中点,
∴FC=DF=FE,
∵∠CDF=∠A=60°,
∴△DFC是等边三角形,
∴DF=DC=FC,
∵△ADC是等边三角形,
∴AD=AC=DC,
∴AD=AC=FC=DF,
∴四边形ACFD是菱形
【解析】(1)利用旋转的性质得出AC=CD,进而得出△ADC是等边三角形,即可得出∠ACD的度数;(2)利用直角三角形的性质得出FC=DF,进而得出AD=AC=FC=DF,即可得出答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有这样一个问题:探究函数y=
 x2+
x2+  的图象与性质.
的图象与性质.
小东根据学习函数的经验,对函数y= x2+
x2+  的图象与性质进行了探究.
的图象与性质进行了探究.
下面是小东的探究过程,请补充完整:
(1)函数y= x2+
x2+  的自变量x的取值范围是
的自变量x的取值范围是
(2)下表是y与x的几组对应值.x
…
﹣3
﹣2
﹣1
﹣

﹣



1
2
3
…
y
…


﹣

﹣

﹣





m
…
求m的值;
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(4)进一步探究发现,该函数图象在第一象限内的最低点的坐标是(1, ),结合函数的图象,写出该函数的其它性质(一条即可) .
),结合函数的图象,写出该函数的其它性质(一条即可) . -
科目: 来源: 题型:
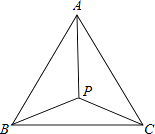
查看答案和解析>>【题目】已知:如图,P为等边△ABC内一点,∠APB=113°,∠APC=123°,试说明:以AP,BP,CP为边长可以构成一个三角形,并确定所构成三角形的各内角的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】∠ACD是△ABC的外角,BE平分∠ABC,CE平分∠ACD,且BE、CE交于点E.
(1)若∠A=58,求:∠E的度数.
(2)猜想∠A与∠E的关系,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】取一副三角板按图1拼接,固定三角板ADC,将三角板ABC绕点A依顺时针方向旋转一个大小为α的角 (0°<α≤45°)得到△ABC′,如图所示.试问:
(1)当α为多少度时,能使得图2中AB∥DC.
(2)连接BD,当0°<α≤45°时,探寻∠DBC′+∠CAC′+∠BDC值的大小变化情况,并给出你的证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,过边长为1的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,则DE的长为( )

A.
 B.
B.  C.
C.  D. 不能确定
D. 不能确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将在Rt△ABC绕其锐角顶点A旋转90°得到在Rt△ADE,连接BE,延长DE、BC相交于点F,则有∠BFE=90°,且四边形ACFD是一个正方形.
(1)判断△ABE的形状,并证明你的结论;
(2)用含b代数式表示四边形ABFE的面积;
(3)求证:a2+b2=c2.

相关试题

