搜索
【题目】如图，两个同心圆的半径分别为4cm和5cm，大圆的一条弦AB与小圆相切，则弦AB的长为（ ） 
A.6cm
B.4cm
C.3cm
D.8cm
参考答案：
【答案】A
【解析】解：如图，连接OC，AO，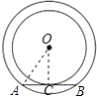 
∵大圆的一条弦AB与小圆相切，
∴OC⊥AB，
∴AC=BC= 
AB，
∵OA=5cm，OC=4cm，
在Rt△AOC中，AC= 
=3cm，
∴AB=2AC=6（cm）．
故选A．
【考点精析】掌握切线的性质定理和圆与圆的位置关系是解答本题的根本，需要知道切线的性质：1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径；两圆之间有五种位置关系：无公共点的，一圆在另一圆之外叫外离，在之内叫内含；有唯一公共点的，一圆在另一圆之外叫外切，在之内叫内切；有两个公共点的叫相交．两圆圆心之间的距离叫做圆心距．两圆的半径分别为R和r，且R≥r，圆心距为P：外离P＞R+r；外切P=R+r；相交R-r＜P＜R+r；内切P=R-r；内含P＜R-r．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在Rt△ABC中∠C=90°，∠A=30°，BC=2，点P，Q，R分别是AB，AC，BC上的动点，PQ+PR+QR的最小值是_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ACB和△ECD都是等腰直角三角形，∠ACB=∠ECD=90°，点D为AB边上一点．
（1）求证：AD2+DB2=ED2；
（2）若BC=
，求四边形ADCE的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】定义：有两条边长的比值为
的直角三角形叫“潜力三角形”．如图，在△ABC中，∠B=90°，D是AB的中点，E是CD的中点，DF∥AE交BC于点F．
（1）设“潜力三角形”较短直角边长为a，斜边长为c，请你直接写出
的值为；
（2）若∠AED=∠DCB，求证：△BDF是“潜力三角形”；
（3）若△BDF是“潜力三角形”，且BF=1，求线段AC的长． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在四边形ABCD中，E、F分别是CD、AB延长线上的点，连结EF，分别交AD、BC于点G、H．若∠1=∠2，∠A=∠C，试说明AD//BC和AB//CD．请完成下面的推理过程，填写理由或数学式:
∵∠1=∠2，∠1=∠AGH（_________）
∴∠2=∠AGH（________）
∴AD//BC（________）
∴∠ADE=∠C（________）
∵∠A=∠C（已知）
∴∠ADE=_______（等量代换）
∴AB//CD（_______）
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算：
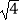﹣|﹣2|+（ 
）﹣2﹣20160 ． -
科目： 来源： 题型：
查看答案和解析>>【题目】景新中学为了进一步丰富学生的课外阅读，欲增购一些课外书，为此对该校一部分学生进行了一次“你最喜欢的书籍”问卷调查（每人只选一项）．根据收集到的数据，绘制成如下统计图（不完整）：请根据图中提供的信息，完成下列问题：
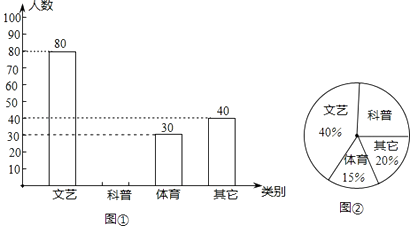
（1）在这次问卷调查中，喜欢“科普书籍”出现的频率为；
（2）在扇形统计图中，喜欢“体育书籍”的所占的圆心角度数为；
（3）如果全校共有学生1500名，请估计该校最喜欢“科普书籍”的学生约有人．
相关试题
