【题目】如图,平行四边形ABCD中,点E、F、G、H分别在AB、BC、CD、AD边上且AE=CG,AH=CF.

(1)求证:四边形EFGH是平行四边形;
(2)如果AB=AD,且AH=AE,求证:四边形EFGH是矩形.
参考答案:
【答案】(1)证明见解析.(2)证明见解析.
【解析】试题分析:(1)易证得△AEH≌△CGF,从而证得BE=DG,DH=BF.故有,△BEF≌△DGH,根据两组对边分别相等的四边形是平行四边形而得证.
(2)由题意知,平行四边形ABCD是菱形,连接AC,BD,则有AC⊥BD,由AB=AD,且AH=AE可证得HE∥BD,同理可得到HG∥AC,故HG⊥HE,又由(1)知四边形HGFE是平行四边形,故四边形HGFE是矩形.
试题解析:证明:(1)在平行四边形ABCD中,∠A=∠C,
又∵AE=CG,AH=CF,
∴△AEH≌△CGF.
∴EH=GF.
在平行四边形ABCD中,AB=CD,AD=BC,
∴AB-AE=CD-CG,AD-AH=BC-CF,
即BE=DG,DH=BF.
又∵在平行四边形ABCD中,∠B=∠D,
∴△BEF≌△DGH.
∴GH=EF.
∴四边形EFGH是平行四边形.
(2)在平行四边形ABCD中,AB∥CD,AB=CD.
设∠A=α,则∠D=180°-α.
∵AE=AH,∴∠AHE=∠AEH=![]() .
.
∵AD=AB=CD,AH=AE=CG,
∴AD-AH=CD-CG,即DH=DG.
∴∠DHG=∠DGH=![]() .
.
∴∠EHG=180°-∠DHG-∠AHE=90°.
又∵四边形EFGH是平行四边形,
∴四边形EFGH是矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2分)矩形的一内角平分线把矩形的一条边分成3和5两部分,则该矩形的周长是()
A. 16 B. 22或16 C. 26 D. 22或26
-
科目: 来源: 题型:
查看答案和解析>>【题目】矩形的一个内角平分线把矩形的一条边分成3cm和5cm两部分,则矩形的周长( )
A. 16cm B. 22cm和16cm C. 26cm D. 22cm和26cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】矩形的对角线所成的角之一是65°,则对角线与各边所成的角度是( )
A. 57.5° B. 32.5° C. 57.5°,23.5° D. 57.5°,32.5°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( )
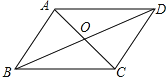
A.
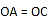 ,
,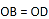 B.
B. 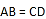 ,
,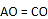
C.
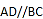 ,
,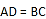 D.
D. 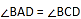 ,
,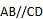
-
科目: 来源: 题型:
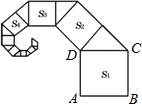
查看答案和解析>>【题目】如图,正方形ABCD的边长为2,其面积标记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,…按照此规律继续下去,则S2016的值为( )
A. (
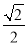 )2013B. (
)2013B. (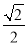 )2014C. (
)2014C. (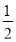 )2013D. (
)2013D. (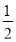 )2014
)2014 -
科目: 来源: 题型:
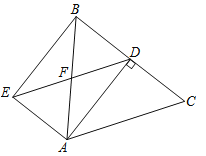
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=5,BC=6,AD为BC边上的高,过点A作AE∥BC,过点D作DE∥AC,AE与DE交于点E,AB与DE交于点F,连结BE.求四边形AEBD的面积
相关试题

