【题目】如图,点M,N分别是正五边形ABCDE的边BC、CD上的点,且BM=CN,AM交BN于点P
(1)求正五边形ABCDE每个内角的度数;
(2)求证:△ABM≌△BCN
(3)求∠APN的度数.
参考答案:
【答案】
(1)解:正五边形的每一个内角相等
∴正五边形的每一个内角为:![]() =180°
=180°
(2)解:∵正五边形ABCDE
∴AB=BC,∠ABM=∠BCN,
在△ABM和△BCN中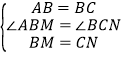
![]()
∴△ABM≌△BCN(SAS).
(3)解:∵△ABM≌△BCN
∴∠BAM=∠CBN
∵∠APN=∠BAM+∠ABP
∴∠APN=∠CBN+∠ABP=∠ABC=108°。
【解析】(1)根据正五边形的每一个内角相等,用正五边形的内角和除以5,计算即可。
(2)根据正五边形的性质得出AB=BC,∠ABM=∠BCN,再根据全等三角形的判定证明△ABM≌△BCN即可。
(3)根据全等三角形的性质得出∠BAM=∠CBN,再根据∠APN=∠BAM+∠ABP,证得∠APN=∠ABC,即可得出答案。
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF

(1)求证:Rt△ABE≌Rt△CBF;
(2)若∠CAE=30。 , 求∠ACF的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于X的一元二次方程为:
 。
。(1)当方程有两实数根时,求
 的取值范围;
的取值范围;(2)任取一个
 值,求出方程的两个不相等实数根。
值,求出方程的两个不相等实数根。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
 的图象过点C(0,1),顶点为Q(2,3),点D在x轴正半轴上,线段OD=OC.
的图象过点C(0,1),顶点为Q(2,3),点D在x轴正半轴上,线段OD=OC.(1)求抛物线的解析式;
(2)抛物线上是否存在点M,使得⊿CDM是以CD为直角边的直角三角形?若存在,请求出M点的坐标;若不存在,请说明理由.
(3)将直线CD绕点C逆时针方向旋转45°所得直线与抛物线相交于另一点E,,连接QE.若点P是线段QE上的动点,点F是线段OD上的动点,问:在P点和F点的移动过程中,△PCF的周长是否存在最小值?若存在,求出这个最小值,若不存在,请说明理由。


-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中,点P的坐标为(﹣5,3),则点P关于原点对称的点的坐标是( )
A. (5,﹣3) B. (﹣5,﹣3) C. (3,﹣5) D. (﹣3,5)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠A=∠B+∠C,∠B=2∠C﹣6°,则∠C的度数为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AB的垂直平分线交AB于N,交AC于点M
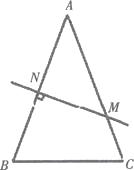
(1)若∠B=70。 , 求∠NMA.
(2)连接MB,若AB=8cm,△MBC的周长是14cm,求BC的长.
(3)在(2)的条件,直线MN上是否存在点P,使由P,B,C构成的△PBC的周长值最小?若存在,标出点P的位置并求△PBC的周长最小值;若不存在,说明理由.
相关试题

