【题目】如图，在等腰三角形ABC中，AC=BC，分别以BC和AC为直角边向上作等腰直角三角形△BCD和△ACE，AE与BD相交于点F，连接CF并延长交AB于点G．求证：CG垂直平分AB．

参考答案：

【答案】证明：∵CA=CB
∴∠CAB=∠CBA
∵△AEC和△BCD为等腰直角三角形，
∴∠CAE=∠CBD=45°，∠FAG=∠FBG，
∴∠FAB=∠FBA，
∴AF=BF，
在三角形ACF和△CBF中，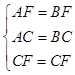
，
∴△AFC≌△BCF（SSS），
∴∠ACF=∠BCF
∴AG=BG，CG⊥AB（三线合一），
即CG垂直平分AB
【解析】求证△AFC≌△CEB可得∠ACF=∠BCF，根据等腰三角形底边三线合一即可解题．
【考点精析】通过灵活运用等腰直角三角形和线段垂直平分线的性质，掌握等腰直角三角形是两条直角边相等的直角三角形；等腰直角三角形的两个底角相等且等于45°；垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线；线段垂直平分线的性质定理：线段垂直平分线上的点和这条线段两个端点的距离相等即可以解答此题．

关闭