Question

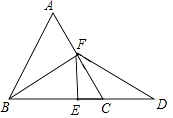
【题目】如图，在等边△ABC中，点F是AC边上一点，延长BC到点D，使BF=DF，若CD=CF，求证：

（1）点F为AC的中点；
（2）过点F作FE⊥BD，垂足为点E，请画出图形并证明BD=6CE．

Answer 1

【答案】
（1）解：∵△ABC为等边三角形，

∴∠ABC=∠ACB=60°，

∵CF=CD，

∴∠CFD=∠D，

∴∠ACB=2∠D，即∠D= ∠ACB=30°，

∵FB=FD，

∴∠FBD=∠D=30°，

∴BF平分∠ABC，

∴AF=CF，即点F为AC的中点

（2）解：如图，

在Rt△EFC中，CF=2CE，

而CD=CF，

∴CF=2CE，

在Rt△BCF中，BC=2CF，

∴BC=4CE，

∴BD=6CE．

【解析】（1）根据等边三角形的性质得∠ABC=∠ACB=60°，利用∠CFD=∠D，则根据三角形外角性质得到∠ACB=2∠D，即∠D= ∠ACB=30°，然后利用FB=FD得到∠FBD=∠D=30°，则BF平分∠ABC，于是根据等边三角形的性质可得到点F为AC的中点；（2）如图，过点F作FE⊥BD于E，利用含30度的直角三角形三边的关系得到CF=2CE，而CD=CF，则CF=2CE，再利用BC=2CF，所以BD=6CE．
【考点精析】解答此题的关键在于理解等边三角形的性质的相关知识，掌握等边三角形的三个角都相等并且每个角都是60°．