【题目】数学实验室:

制作4张全等的直角三角形纸片(如图1),把这4张纸片拼成以弦长c为边长的正方形构成“弦图”(如图2),古代数学家利用“弦图”验证了勾股定理.
探索研究:
(1)小明将“弦图”中的2个三角形进行了运动变换,得到图3,请利用图3证明勾股定理;
数学思考:
(2)小芳认为用其它的方法改变“弦图”中某些三角形的位置,也可以证明勾股定理.请你想一种方法支持她的观点(先在备用图中补全图形,再予以证明).
参考答案:
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)通过图形的面积的两种计算方法,即可得出结果;
(2)通过大正方形面积的两种计算方法,即可得出结果.
(1)解:如图3所示,
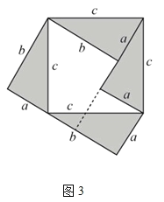
图形的面积表示为:![]() ,
,
图形的面积也可表示:![]() ,
,
∴a2b2abc2ab,
∴a2b2c2
(2)解:如图4所示,
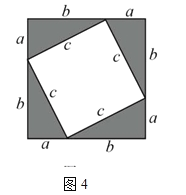
大正方形的面积表示为:ab2,
大正方形的面积也可以表示为:![]() ,
,
∴![]() ,
,
∴a2b22abc22ab,
∴a2b2c2;
-
科目: 来源: 题型:
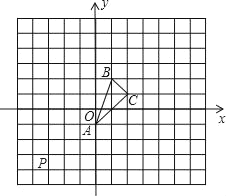
查看答案和解析>>【题目】如图是网格图,每个小正方形的边长均为1.△ABC它在坐标平面内平移,得到△PEF,点A平移后落在点P的位置上.
(1)请你在图中画出△PEF,并写出顶点P、E、F的坐标;
(2)说出△PEF是由△ABC分别经过怎样的平移得到的?
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=﹣x2+mx的图象如图,对称轴为直线x=2,若关于x的一元二次方程﹣x2+mx﹣t=0(t为实数)在1<x<5的范围内有解,则t的取值范围是( )

A.t>﹣5
B.﹣5<t<3
C.3<t≤4
D.﹣5<t≤4 -
科目: 来源: 题型:
查看答案和解析>>【题目】将一幅三角板拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F.

(1)求证:CF∥AB.
(2)求∠DFC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题:①两条直线相交,一个角的两邻补角相等,则这两条直线垂直;②同位角相等;③点(5,6)与点(6,5)表示同一点;④若两个同旁内角互补,则它们的角平分线互相垂直;⑤点(
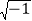 ,5)在第二象限.其中假命题的个数为( )
,5)在第二象限.其中假命题的个数为( )A. 4B. 3C. 2D. 1
-
科目: 来源: 题型:
查看答案和解析>>【题目】代数式ax2+bx+c(a≠0,a,b,c是常数)中,x与ax2+bx+c的对应值如下表:
x
﹣1
﹣

0

1

2

3
ax2+bx+c
﹣2
﹣

1

2

1
﹣

﹣2
请判断一元二次方程ax2+bx+c=0(a≠0,a,b,c是常数)的两个根x1 , x2的取值范围是下列选项中的( )
A.﹣ <x1<0,
<x1<0,  <x2<2
<x2<2
B.﹣1<x1<﹣ ,2<x2<
,2<x2< 
C.﹣ <x1<0,2<x2<
<x1<0,2<x2< 
D.﹣1<x1<﹣ ,
,  <x2<2
<x2<2 -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,D是BC的中点,以AC为腰向外作等腰直角△ACE,∠EAC=90°,连接BE,交AD于点F,交AC于点G.
(1)求证:∠AEB=∠ACF;
(2)求证:EF2BF22AC2.

相关试题

