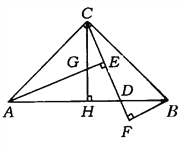
【题目】如图,在等腰Rt△ABC中,∠C=90°,D是斜边上AB上任一点,AE⊥CD于E,BF⊥CD交CD的延长线于F,CH⊥AB于H点,交AE于G.
(1)试说明AH=BH
(2)求证:BD=CG.
(3)探索AE与EF、BF之间的数量关系
参考答案:
【答案】(1)见解析;(2)见解析;(3)AE=EF+BF,理由见解析
【解析】试题分析:
(1)根据等腰三角形的三线合一证明;
(2)证明△ACG≌△CBD,根据全等三角形的性质证明;
(3)证明△ACE≌△CBF即可.
试题解析:
(1)∵AC=BC,CH⊥AB∴AH=BH
(2)∵ABC为等腰直角三角形,且CH⊥AB
∴∠ACG=45°
∵∠CAG+∠ACE=90°,∠BCF+∠ACE=90°
∴∠CAG=∠BCF
在△ACG和△CBD中
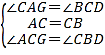
∴△ACG≌△CBD(ASA)
∴BD=CG
(3)AE=EF+BF
理由如下:
在△ACE和△CBF中,
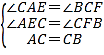
∴△ACE≌△CBF,
∴AE=CF,CE=BF,
∴AE=CF=CE+EF=BF+EF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若(a+b)2=5,(a﹣b)2=3,则a2+b2=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个数的算术平方根和立方根都等于它本身,则这个数一定是( )
A.0或1
B.1或-1
C.0或±1
D.0 -
科目: 来源: 题型:
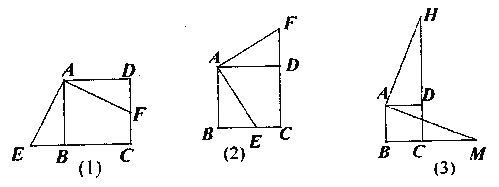
查看答案和解析>>【题目】(1)观察发现:四边形ABCD是正方形,点E是直线BC上的动点,连结AE,过点A作AF⊥AE交直线CD于F.当点E位于点B的左侧时,如图(1).观察线段AB.BE.CF之间有何数量关系?请直接写出线段AB.BE.CF之间的数量关系.
(2)拓展探究:当点E位于点B的右侧时,如图(2),线段AB.BE.CF之间有何数量关系?并说明理由.
(3)迁移应用:如图(3),正方形ABCD的边长为2cm时,线段CM=3cm,直接写出线段CH的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】A,B两地相距20 km,甲、乙两人都从A地去B地,如图,l1和l2分别表示甲、乙两人所走路程s(km)与时间t(h)之间的关系,下列说法:①乙晚出发1 h;②乙出发3 h后追上甲;③甲的速度是4 km/h;④乙先到达B地.其中正确的个数是( )

A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线y=(3﹣π)x经过的象限是( )
A.一、二象限
B.一、三象限
C.二、三象限
D.二、四象限 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,左右两幅图案关于y轴对称,右图案中的左右眼睛的坐标分别是(2,3),(4,3),嘴角左右端点的坐标分别是(2,1),(4,1).
(1)试确定左图案中的左右眼睛和嘴角左右端点的坐标;
(2)从对称的角度来考虑,说一说你是怎样得到的.

相关试题

