【题目】如图,直线l3,l4与l1,l2分别相交于点A、B、C、D,且∠1+∠2=180°.
(1)直线l1与l2平行吗?为什么?
(2)点E在线段AD上,∠ABE=30°,∠BEC=62°,求∠DCE的度数.

参考答案:
【答案】(1)见解析;(2)∠DCE=32°.
【解析】
(1)根据平行线的判定解答即可;
(2)过点E作EF∥AB交BC于点F,利用平行线的判定和性质解答即可.
(1)直线l1与l2平行,
∵∠1+∠BAE=180°,∠1+∠2=180°,
∴∠2=∠BAE,
∴l1∥l2.
(2)过点E作EF∥AB交BC于点F,

可得:∠BEF=∠ABE=30°,
∴∠FEC=62°﹣30°=32°,
∵l1∥l2,
∴EF∥CD,
∴∠DCE=∠FEC=32°.
-
科目: 来源: 题型:
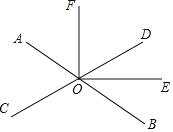
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,OE平分∠BOD
(1)若∠AOC=60°,求∠BOE的度数;
(2)若OF平分∠AOD,试说明OE⊥OF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某天小明骑自行车上学,途中因自行车发生故障,修车耽误了一段时间后继续骑行,按时赶到了学校.图中描述了他上学的途中离家距离
 (米)与离家时间
(米)与离家时间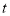 (分钟)之间的函数关系.下列说法中正确的个数是( )
(分钟)之间的函数关系.下列说法中正确的个数是( )(1)修车时间为15分钟;
(2)学校离家的距离为4000米;
(3)到达学校时共用时间为20分钟;
(4)自行车发生故障时离家距离为2000米.

A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】在边长为1的小正方形网格中,△AOB的顶点均在格点上.
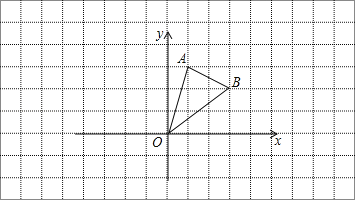
(1)B点关于y轴的对称点坐标为 ;
(2)将△AOB向左平移3个单位长度,再向上平移2个单位长度得到△A1O1B1,请画出△A1O1B1;
(3)在(2)的条件下,△AOB边AB上有一点P的坐标为(a,b),则平移后对应点P1的坐标为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某庄有甲、乙两家草莓采摘园的草莓销售价格相同,春节期间,两家采摘园将推出优惠方案,甲园的优惠方案是:游客进园需购买门票,采摘的草莓六折优惠;乙园的优惠方案是:游客进园不需购买门票,采摘的草莓超过一定数量后,超过部分打折优惠.优惠期间,某游客的草莓采摘量为
 (千克),在甲园所需总费用为
(千克),在甲园所需总费用为 (元),在乙园所需总费用为
(元),在乙园所需总费用为 (元),
(元), 、
、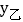 与
与 之间的函数关系如图所示.
之间的函数关系如图所示.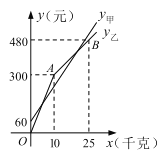
(1)甲采摘园的门票是_____元,两个采摘园优惠前的草莓单价是每千克____元;
(2)当
 时,求
时,求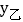 与
与 的函数表达式;
的函数表达式;(3)游客在“春节期间”采摘多少千克草莓时,甲、乙两家采摘园的总费用相同.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场销售同型号A、B两种品牌节能灯管,它们进价相同,A品牌售价可变,最低售价不能低于进价,最高利润不超过4元,B品牌售价不变.它们的每只销售利润与每周销售量如下表:(售价=进价+利润)

(1)当A品牌每周销售量为300只时,B品牌每周销售多少只?
(2)A品牌节能灯管每只利润定为多少元时?可获得最大总利润,并求最大总利润.
-
科目: 来源: 题型:
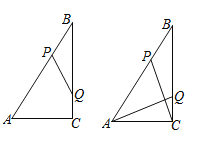
查看答案和解析>>【题目】如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.
(1)若△BPQ与△ABC相似,求t的值;
(2)当t为何值时,四边形ACQP的面积最小,最小值是多少?
(3)连接AQ,CP,若AQ⊥CP,求t的值.
相关试题

