搜索
【题目】（2016山东省泰安市）某学校将为初一学生开设ABCDEF共6门选修课，现选取若干学生进行了“我最喜欢的一门选修课”调查，将调查结果绘制成如图统计图表（不完整）
根据图表提供的信息，下列结论错误的是（ ）
A. 这次被调查的学生人数为400人
B. 扇形统计图中E部分扇形的圆心角为72°
C. 被调查的学生中喜欢选修课E、F的人数分别为80，70
D. 喜欢选修课C的人数最少
参考答案：
【答案】D
【解析】
试题通过计算得出选项A、B、C正确，选项D错误，即可得出结论．
被调查的学生人数为60÷15%=400（人），∴选项A正确；
扇形统计图中D的圆心角为
×360°=90°，∵
×360°=36°，360°（17.5%+15%+12.5%）=162°，∴扇形统计图中E的圆心角=360°﹣162°﹣90°﹣36°=72°， ∴选项B正确；
∵400×
=80（人），400×17.5%=70（人），∴选项C正确；
∵12.5%＞10%， ∴喜欢选修课A的人数最少，∴选项D错误；
-
科目： 来源： 题型：
查看答案和解析>>【题目】如果一元一次方程的解是一元一次不等式组的解，则称该一元一次方程为该不等式组的关联方程．
（1）在方程①x﹣（3x+1）＝﹣5；②
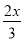+1＝0；③3x﹣1＝0 中，不等式组
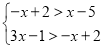的关联方程是 （填序号）；（2）若不等式组
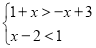的某个关联方程 2x-m=1 的解是整数, 求 m 的值；（3）若方程
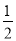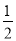﹣ x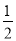＝ x，3+x＝2（x+
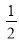）都是关于 x 的不等式组
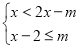的关联方程，直接写出 m的取值范围． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点O为Rt△ABC斜边AB上的一点，以OA为半径的⊙O与边BC交于点D，与边AC交于点E，连接AD，且AD平分∠BAC．
（1）试判断BC与⊙O的位置关系，并说明理由；
（2）若∠BAC=60°，OA=2，求阴影部分的面积（结果保留π）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点A在直线l外，点B在直线l上．
（1）在l上求作一点C，在l外求作一点D，使得以A、B、C、D为顶点的四边形是菱形；（要求：用直尺和圆规作出所有大小不同的菱形）
（2）连接AB，若AB＝5，且点A到直线l的距离为4，通过计算，找出（1）中面积最小的菱形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】若四边形的一条对角线把四边形分成两个等腰三角形，则这条对角线叫做这个四边形的“巧分线”，这个四边形叫“巧妙四边形”，若一个四边形有两条巧分线，则称为“绝妙四边形”．
（1）下列四边形一定是巧妙四边形的是 ；（填序号点①平行四边形；②矩形；③菱形；④正方形．
初步应用
（2）在绝妙四边形ABCD中，AC垂直平分BD，若∠BAD＝80°，则∠BCD＝ ；
深入研究
（3）如图，在梯形ABCD中，AD∥BC，AB＝AD＝CD，∠B＝72°．求证：梯形ABCD是绝妙四边形．
（4）在巧妙四边形ABCD中，AB＝AD＝CD，∠A＝90°，AC是四边形ABCD的巧分线，请直接写出∠BCD的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知A、B、C、D是⊙O上的四点，
，AC是四边形ABCD的对角线（1）如图1，连结BD，若∠CDB=60°，求证：AC是∠DAB的平分线；
（2）如图2，过点D作DE⊥AC，垂足为E，若AC=7，AB=5，求线段AE的长度．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在矩形ABCD中，AB=6cm，BC=12cm，点P从点A出发，沿AB边向点B以每秒1cm的速度移动，同时点Q从点B出发沿BC边向点C以每秒2cm的速度移动P、Q两点在分别到达B、C两点后就停止移动，设两点移动的时间为t秒，回答下列问题：
（1）如图1，当t为几秒时，△PBQ的面积等于5cm2？
（2）如图2，当t=
秒时，试判断△DPQ的形状，并说明理由；（3）如图3，以Q为圆心，PQ为半径作⊙Q．
①在运动过程中，是否存在这样的t值，使⊙Q正好与四边形DPQC的一边（或边所在的直线）相切？若存在，求出t值；若不存在，请说明理由；
②若⊙Q与四边形DPQC有三个公共点，请直接写出t的取值范围。
相关试题
