【题目】如图,在4×9的方格图中,ABCD的顶点均在格点上,按下列要求作图: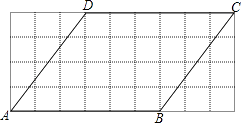
(1)在CD边上找一格点E,使得AE平分∠DAB.
(2)在CD边上找一格点F,使得BF⊥AE.
参考答案:
【答案】
(1)解:如图,AE就是所求图形;
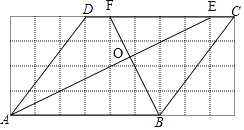
(2)解:如图,BF就是所求图形

【解析】(1)在DC上取DE=DA=5,可知∠DAE=∠DEA,由DC∥AB知∠DEA=∠BAE,从而得出∠DAE=∠BAE= ![]() ∠DAB;(2)在CD上取CF=CB,与(1)同理可得∠ABF=
∠DAB;(2)在CD上取CF=CB,与(1)同理可得∠ABF= ![]() ∠ABC,根据∠DAB+∠ABC=180°可得∠BAE+∠ABF=90°,即可得出BF⊥AE.
∠ABC,根据∠DAB+∠ABC=180°可得∠BAE+∠ABF=90°,即可得出BF⊥AE.
【考点精析】解答此题的关键在于理解角平分线的性质定理的相关知识,掌握定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上,以及对线段垂直平分线的性质的理解,了解垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“重百”、“沃尔玛”两家超市出售同样的保温壶和水杯,保温壶和水杯在两家超市的售价分别一样.已知买1个保温壶和1个水杯要花费60元,买2个保温壶和3个水杯要花费130元.
(1)请问:一个保温壶与一个水杯售价各是多少元;(列方程组求解)
(2)为了迎接“五一劳动节”,两家超市都在搞促销活动,“重百”超市规定:这两种商品都打九折;“沃尔玛”超市规定:买一个保温壶赠送一个水杯.若某单位想要买4个保温壶和15个水杯,如果只能在一家超市购买,请问选择哪家超市购买更合算,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在平面直角坐标系中,O为坐标原点,△OAB的顶点A、B的坐标分别是A(0,5),B(3,1),过点B画BC⊥AB交直线y=﹣m(m>
 )于点C,连结AC,以点A为圆心,AC为半径画弧交x轴负半轴于点D,连结AD、CD.
)于点C,连结AC,以点A为圆心,AC为半径画弧交x轴负半轴于点D,连结AD、CD.
(1)求证:△ABC≌△AOD;
(2)设△ACD的面积为S,求S关于m的函数关系式;
(3)若四边形ABCD恰有一组对边平行,求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知A(0,a),B(b,0),C(b,4)三点,其中a,b满足关系式a=
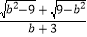 +2.若在第二象限内有一点P(m,1),使四边形ABOP的面积与三角形ABC的面积相等,则点P的坐标为( )
+2.若在第二象限内有一点P(m,1),使四边形ABOP的面积与三角形ABC的面积相等,则点P的坐标为( )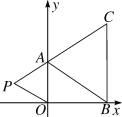
A. (-3,1) B. (-2,1) C. (-4,1) D. (-2.5,1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠B=45°,AD⊥BC于点D,以D为圆心DC为半径作⊙D交AD于点G,过点G作⊙D的切线交AB于点F,且F恰好为AB中点.
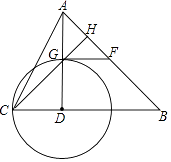
(1)求tan∠ACD的值.
(2)连结CG并延长交AB于点H,若AH=2,求AC的长. -
科目: 来源: 题型:
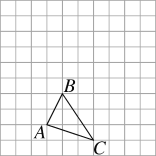
查看答案和解析>>【题目】如图,已知单位长度为1的方格中有三角形ABC.
(1)请画出三角形ABC向上平移3格再向右平移2格所得的三角形A′B′C′;
(2)请以点A为坐标原点建立平面直角坐标系(在图中画出),然后写出点B,B′的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形ABCD在坐标平面内,点A的坐标是A(
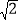 ,1),且边AB,CD与x轴平行,边AD,BC与y轴平行,AB=4,AD=2.
,1),且边AB,CD与x轴平行,边AD,BC与y轴平行,AB=4,AD=2.(1)求B,C,D三点的坐标;
(2)怎样平移,才能使A点与原点O重合?
相关试题

