【题目】如图,直角三角形DEF中,∠DFE=90°在直角三角形外面作正方形ABDE,CDFI,EFGH的面积分别为25,9,16.△AEH,△BDC,△GFI的面积分别为S1,S2,S3,则S1+S2+S3=( )

A.18B.21C.23.5D.26
参考答案:
【答案】A
【解析】
过点A作AM⊥EH,交HE的延长线于点M,由正方形的性质可得AE=DE=5,EF=FH=4,DF=FI=3,∠AED=∠HEF=90°=∠MEF,由“AAS”可证△AME≌△DFE,可得AM=DF,即可得S1=S△DEF,同理可得S2=S△DEF,S3=S△DEF,即可求解.
解:如图,过点A作AM⊥EH,交HE的延长线于点M,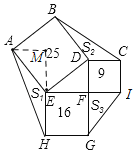
∵正方形ABDE,CDFI,EFGH的面积分别为25,9,16,
∴AE=DE=5,EF=FH=4,DF=FI=3,∠AED=∠HEF=90°=∠MEF
∴∠AEM=∠DEF,且∠AME=∠DFE,AE=DE
∴△AME≌△DFE(AAS)
∴AM=DF
∵S1=![]() EH×AM,S△DEF=
EH×AM,S△DEF=![]() ×EF×DF
×EF×DF
∴S1=S△DEF,
同理可得:S2=S△DEF,S3=S△DEF,
∴S1+S2+S3=3S△DEF=3×![]() ×4×3=18
×4×3=18
故选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长方形ABCD中,AB=3,BC=5,在CD上任取一点E,连接BE,将△BCE沿BE折叠,使点C恰好落在AD边上的点F处,则CE的长为( )

A.4B.5C.
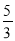 D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
 的图象如图所示,则下列结论:①
的图象如图所示,则下列结论:① ;②
;② ;③
;③ ;④
;④ .其中正确的结论是( )
.其中正确的结论是( )
A. ①② B. ②③ C. ③④ D. ②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线
 经过
经过 、
、 两点.
两点.
 求抛物线的解析式和顶点坐标;
求抛物线的解析式和顶点坐标; 当
当 时,求
时,求 的取值范围;
的取值范围; 点
点 为抛物线上一点,若
为抛物线上一点,若 ,求出此时点
,求出此时点 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读下列一段文字,再回答后面的问题.
已知在平面内两点P1(x1,y1),P2(x2,y2),这两点间的距离P1P2=
 ,同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为|x2﹣x1|或|y2﹣y1|.
,同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为|x2﹣x1|或|y2﹣y1|.(1)已知A(3,3),B(﹣2,﹣1),试求A,B两点间的距离;
(2)已知A,B在平行于y轴的直线上,点A的纵坐标为7,点B的纵坐标为﹣2,试求A,B两点间的距离;
(3)已知一个三角形各顶点坐标为A(0,5),B(﹣3,2),C(3,2),你能判断此三角形的形状吗?说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
 与
与 轴仅有一个公共点
轴仅有一个公共点 ,经过点
,经过点 的直线交该抛物线于点
的直线交该抛物线于点 ,交
,交 轴于点
轴于点 ,且点
,且点 是线段
是线段 的中点.
的中点.
 求这条抛物线对应的函数解析式;
求这条抛物线对应的函数解析式; 求直线
求直线 对应的函数解析式.
对应的函数解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】(题文)如图
 ,在平面直角坐标系
,在平面直角坐标系 中,抛物线
中,抛物线 经过点
经过点 ,顶点为点
,顶点为点 ,点
,点 为抛物线上的一个动点,
为抛物线上的一个动点, 是过点
是过点 且垂直于
且垂直于 轴的直线,过
轴的直线,过 作
作 ,垂足为
,垂足为 ,连接
,连接 .
. 求抛物线的解析式,并写出其顶点
求抛物线的解析式,并写出其顶点 的坐标;
的坐标; ①当
①当 点运动到
点运动到 点处时,计算:
点处时,计算: ________,
________, ________,由此发现,
________,由此发现, ________
________ (填“
(填“ ”、“
”、“ ”或“
”或“ ”);
”);②当
 点在抛物线上运动时,猜想
点在抛物线上运动时,猜想 与
与 有什么数量关系,并证明你的猜想;
有什么数量关系,并证明你的猜想; 如图
如图 ,设点
,设点 ,问是否存在点
,问是否存在点 ,使得以
,使得以 ,
, ,
, 为顶点的三角形与
为顶点的三角形与 相似?若存在,求出
相似?若存在,求出 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.

相关试题

