【题目】如图,已知抛物线![]() 经过
经过![]() 、
、![]() 两点.
两点.

![]() 求抛物线的解析式和顶点坐标;
求抛物线的解析式和顶点坐标;
![]() 当
当![]() 时,求
时,求![]() 的取值范围;
的取值范围;
![]() 点
点![]() 为抛物线上一点,若
为抛物线上一点,若![]() ,求出此时点
,求出此时点![]() 的坐标.
的坐标.
参考答案:
【答案】![]() 顶点坐标为
顶点坐标为![]() ;
; ![]()
![]() 点坐标为
点坐标为![]() 或
或![]() .
.
【解析】
本题为二次函数的综合应用,已知二次函数的两个点用涉及待定系数法求解一小题、根据二次函数的性质求解二小题、用方程思想及分类讨论思想解决三小题.
![]() 把
把![]() 、
、![]() 分别代入
分别代入![]() 中,
中,
得:![]() ,解得:
,解得:![]() ,
,
∴抛物线的解析式为![]() .
.
∵![]() ,
,
∴顶点坐标为![]() .
.
(2) ∵![]() ,
,
∴抛物线开口向上,对称轴为x=1,
∴当x<1时,y随x的增大而减小,当x>1时,y随x的增大而增大,
∴当0<x<1时,当x=0时,y有最大值为-3,当x=1时,y有最小值为-4,
当1<x<3时,当x=3时,y有最大值为0,当x=1时,y有最小值为-4,
∴当0<x<3时,-4<y<0;
![]() 由图可得当
由图可得当![]() 时,
时,![]() .;
.; ![]() ∵
∵![]() 、
、![]() ,
,
∴![]() .
.
设![]() ,则
,则![]() ,
,
∴![]() ,
,
∴![]() .
.
①当![]() 时,
时,![]() ,解得:
,解得:![]() ,
,![]() ,
,
此时![]() 点坐标为
点坐标为![]() 或
或![]() ;
;
②当![]() 时,
时,![]() ,方程无解;
,方程无解;
综上所述,![]() 点坐标为
点坐标为![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆汽车和一辆摩托车分别从A,B两地去同一个城市,它们离A地的路程随时间变化的图象如图所示.则下列结论:①摩托车比汽车晚到1h;②A,B两地的路程为20km;③摩托车的速度为45km/h,汽车的速度为60km/h;④汽车出发1小时后与摩托车相遇,此时距B地40千米.其中正确结论的个数是( )
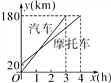
A. 2个 B. 3个 C. 4个 D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长方形ABCD中,AB=3,BC=5,在CD上任取一点E,连接BE,将△BCE沿BE折叠,使点C恰好落在AD边上的点F处,则CE的长为( )

A.4B.5C.
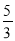 D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
 的图象如图所示,则下列结论:①
的图象如图所示,则下列结论:① ;②
;② ;③
;③ ;④
;④ .其中正确的结论是( )
.其中正确的结论是( )
A. ①② B. ②③ C. ③④ D. ②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直角三角形DEF中,∠DFE=90°在直角三角形外面作正方形ABDE,CDFI,EFGH的面积分别为25,9,16.△AEH,△BDC,△GFI的面积分别为S1,S2,S3,则S1+S2+S3=( )

A.18B.21C.23.5D.26
-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读下列一段文字,再回答后面的问题.
已知在平面内两点P1(x1,y1),P2(x2,y2),这两点间的距离P1P2=
 ,同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为|x2﹣x1|或|y2﹣y1|.
,同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为|x2﹣x1|或|y2﹣y1|.(1)已知A(3,3),B(﹣2,﹣1),试求A,B两点间的距离;
(2)已知A,B在平行于y轴的直线上,点A的纵坐标为7,点B的纵坐标为﹣2,试求A,B两点间的距离;
(3)已知一个三角形各顶点坐标为A(0,5),B(﹣3,2),C(3,2),你能判断此三角形的形状吗?说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
 与
与 轴仅有一个公共点
轴仅有一个公共点 ,经过点
,经过点 的直线交该抛物线于点
的直线交该抛物线于点 ,交
,交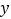 轴于点
轴于点 ,且点
,且点 是线段
是线段 的中点.
的中点.
 求这条抛物线对应的函数解析式;
求这条抛物线对应的函数解析式; 求直线
求直线 对应的函数解析式.
对应的函数解析式.
相关试题

