【题目】平面直角坐标系 ![]() 中,
中, ![]() 是坐标原点。已知A(0,
是坐标原点。已知A(0, ![]() ),B(1,0),C(6,
),B(1,0),C(6, ![]() ),有一抛物线恰好经过这三点.
),有一抛物线恰好经过这三点.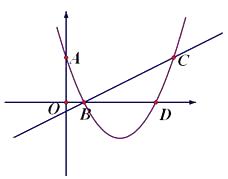
(1)求该抛物线解析式;
(2)若抛物线交 ![]() 轴的另一交点为D,那么抛物线上是否存在一点P,使得
轴的另一交点为D,那么抛物线上是否存在一点P,使得 ![]() ,若存在,求出P的坐标,若不存在,请说明理由。
,若存在,求出P的坐标,若不存在,请说明理由。
参考答案:
【答案】
(1)解:依题可设抛物线解析式为: y=ax2+bx+c(a≠0) ,
∵抛物线经过A,B,C三点,
∴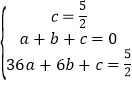 ,
,
∴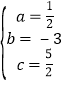 ,
,
∴该抛物线解析式为: y=![]() x23x+
x23x+![]() .
.
(2)解:设直线BC解析式为:y=kx+b,
又∵B(1,0),C(6, ![]() ),
),
∴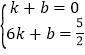 ,
,
∴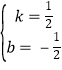 ,
,
∴直线BC的函数解析式为: y=![]() x
x![]() .
.
①若点P在x轴上方,则 OP ∥BC,则OP的函数解析式为 y=![]() x ,
x ,
∴ ,
,
解得 x=![]() ,
,
∴P1(![]() ,
,![]() ),P2(
),P2(![]() ,
,![]() ) .
) .
②若点P在x轴下方,则OP的函数解析式为 y=![]() x ,
x ,
∴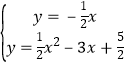 ,
,
解得 x=![]() ,
,
∴ P3(![]() ,
,![]() ),P4(
),P4(![]() ,
,![]() ) .
) .
综上所述: P1(![]() ,
,![]() ),P2(
),P2(![]() ,
,![]() ) , P3(
) , P3(![]() ,-
,-![]() ),P4(
),P4(![]() ,
,![]() ).
).
【解析】(1)依题可设抛物线解析式为: y=ax2+bx+c(a≠0) ,将A,B,C三点坐标代入抛物线解析式,得到一个三元一次方程组,解之即可求出抛物线解析式.
(2)设直线BC解析式为:y=kx+b,将B(1,0),C(6, ![]() )两点坐标代入,得到一个二元一次方程组,解之即可得到直线BC的解析式;再分两种情况讨论:①若点P在x轴上方,则 OP ∥BC,则OP的函数解析式为 y=
)两点坐标代入,得到一个二元一次方程组,解之即可得到直线BC的解析式;再分两种情况讨论:①若点P在x轴上方,则 OP ∥BC,则OP的函数解析式为 y=![]() x ,②若点P在x轴下方,则OP的函数解析式为 y=
x ,②若点P在x轴下方,则OP的函数解析式为 y=![]() x ,分别将OP直线方程和抛物线联立解出P点坐标即可.
x ,分别将OP直线方程和抛物线联立解出P点坐标即可.
【考点精析】通过灵活运用确定一次函数的表达式,掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
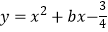 的图像经过点
的图像经过点 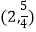 .
.
(1)求这个二次函数的函数解析式;
(2)若抛物线交x轴于A,B两点,交y轴于C点,顶点为D,求以A、B、C、D为顶点的四边形面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图,甲在O点正上方1m的P处发出一球,羽毛球飞行的高度y(m)与水平距离x(m)之间满足函数表达式y=a(x﹣4)2+h,已知点O与球网的水平距离为5m,球网的高度为1.55m.
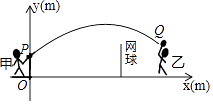
(1)当a=﹣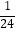 时,①求h的值;
时,①求h的值;
②通过计算判断此球能否过网.
(2)若甲发球过网后,羽毛球飞行到与点O的水平距离为7m,离地面的高度为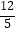 m的Q处时,乙扣球成功,求a的值.
m的Q处时,乙扣球成功,求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司生产一种新型生物医药产品,生产成本为2万元/ 吨,每月生产能力为12吨,且生产出的产品都能销售出去.这种产品部分内销,另一部分外销(出口),内销与外销的单价
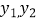 (单位:万元/吨)与销量的关系分别如图1,图2.
(单位:万元/吨)与销量的关系分别如图1,图2.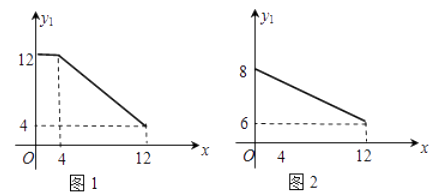
(1)如果该公司内销数量为x(单位:吨),内、外销单价分别为y 1 , y 2 ,求,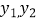 关于x的函数解析式;
关于x的函数解析式;
(2)如果该公司内销数量为x(单位:吨),求内销获得的毛利润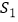 关于x的函数解析式;
关于x的函数解析式;
(3)请设计一种销售方案,使该公司本月能获得最大毛利润,并求出毛利润的最大值.(毛利润=销售收入-生产成本). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线
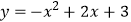 与x轴的交点为A,B(点A在点B的左侧),与y轴的交点为C,连结BC.点M是抛物线上A,C之间的一个动点,过点M作MN∥BC,分别交x轴、抛物线于D,N,过点M作EF⊥x轴,垂足为F,并交直线BC于点E,
与x轴的交点为A,B(点A在点B的左侧),与y轴的交点为C,连结BC.点M是抛物线上A,C之间的一个动点,过点M作MN∥BC,分别交x轴、抛物线于D,N,过点M作EF⊥x轴,垂足为F,并交直线BC于点E,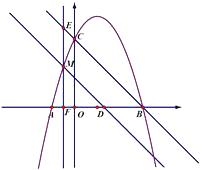
(1)求点A,B,C的坐标.
(2)当点M恰好是EF的中点,求BD的长.
(3)连接DE,记△DEM,△BDE的面积分别为S1,S2 ,当BD=1时,请求S2-S1的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A、D、C、F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加一个条件是( )

A. ∠BCA=∠F; B. ∠B=∠E; C. BC∥EF ; D. ∠A=∠EDF
-
科目: 来源: 题型:
查看答案和解析>>【题目】按下面程序计算,即根据输入的
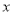 判断
判断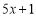 是否大于500,若大于500则输出,结束计算,若不大于500,则以现在的
是否大于500,若大于500则输出,结束计算,若不大于500,则以现在的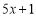 的值作为新的
的值作为新的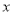 的值,继续运算,循环往复,直至输出结果为止.若开始输入
的值,继续运算,循环往复,直至输出结果为止.若开始输入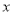 的值为正整数,最后输出的结果为656,则满足条件的所有
的值为正整数,最后输出的结果为656,则满足条件的所有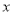 的值是__.
的值是__.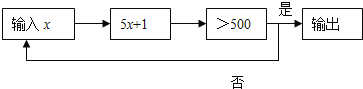
相关试题

