【题目】已知:![]() ,
,![]() 是圆
是圆![]() 的两条直径,连接
的两条直径,连接![]() ,
,![]() .
.
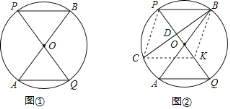
![]() 如图①,求证:
如图①,求证:![]() ,
,![]() ;
;
![]() 如图②,过点
如图②,过点![]() 作
作![]() 于点
于点![]() ,交圆
,交圆![]() 于点
于点![]() ,在
,在![]() 上取一点
上取一点![]() ,使
,使![]() ,
,
求证:四边形![]() 是平行四边形.
是平行四边形.

参考答案:
【答案】(1)证明见解析;(2)证明见解析;
【解析】
(1)由同弧所对的圆周角相等得出∠P=∠A,由OA=OQ得出∠A=∠Q,那么∠P=∠Q,AQ∥PB.根据∠AOQ=∠BOP,得到![]() ,那么AQ=BP;
,那么AQ=BP;
(2)先由垂径定理得出BD=CD,又PD=DK,得出四边形BKCP为菱形,根据菱形的性质得出PB∥CK,再证明CK∥AQ,且CK=AQ,那么四边形AQKC为平行四边形.
证明:![]() ∵
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
![]() ∵
∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() 与
与![]() 互相垂直且平分,
互相垂直且平分,
∴四边形![]() 为菱形;
为菱形;
∴![]() ,且
,且![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,且
,且![]() ,
,
∴四边形![]() 为平行四边形.
为平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如下图所示,直线y=-
 x+3与坐标轴分别交于点A,B,与直线y=x交于点C,线段OA上的点Q以每秒1个单位的速度从点O出发向点A作匀速运动,运动时间为t秒,连结CQ.
x+3与坐标轴分别交于点A,B,与直线y=x交于点C,线段OA上的点Q以每秒1个单位的速度从点O出发向点A作匀速运动,运动时间为t秒,连结CQ.(1)求出点C的坐标;
(2)若△OQC是等腰直角三角形,则t的值为________;
(3)若CQ平分△OAC的面积,求直线CQ对应的函数表达式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在
 中,
中, ,
, ,
, .
. 如图①,将线段
如图①,将线段 绕点
绕点 顺时针旋转
顺时针旋转 ,所得到与
,所得到与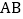 交于点
交于点 ,则
,则 的长
的长 ________;
________; 如图②,点
如图②,点 是边
是边 上一点
上一点 且
且 ,将线段
,将线段 绕点
绕点 旋转,得线段
旋转,得线段 ,点
,点 始终为
始终为 的中点,则将线段
的中点,则将线段 绕点
绕点 逆时针旋转________度时,线段
逆时针旋转________度时,线段 的长最大,最大值为________.
的长最大,最大值为________.
-
科目: 来源: 题型:
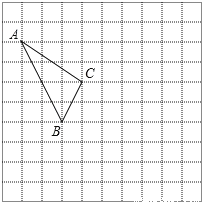
查看答案和解析>>【题目】在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(﹣4,5),(﹣1,3).
(1)请在如图所示的网格平面内作出平面直角坐标系;
(2)写出点B的坐标;
(3)将△ABC向右平移5个单位长度,向下平移2个单位长度,画出平移后的图形△A′B′C′;
(4)计算△A′B′C′的面积﹒
(5)在x轴上存在一点P,使PA+PC最小,直接写出点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校八年级共有三个班,都参加了学校举行的书法绘画大赛,三个班根据初赛成绩分别选出了10名同学参加决赛,这些选手的决赛成绩(满分100分)如下表所示:
决赛成绩(单位:分)
八年1班
80 86 88 80 88 99 80 74 91 89
八年2班
85 85 87 97 85 76 88 77 87 88
八年3班
82 80 78 78 81 96 97 87 92 84
解答下列问题:
(1)请填写下表:
平均数(分)
众数(分)
中位数(分)
八年1班
85.5
87
八年2班
85.5
85
八年3班
78
83
(2)请从以下两个不同的角度对三个班级的决赛成绩进行
①从平均数和众数相结合看(分析哪个班级成绩好些).
②从平均数和中位数相结合看(分析哪个班级成绩好些).
(3)如果在每个班级参加决赛的选手中分别选出3人参加总决赛,你认为哪个班级的实力更强一些?请简要说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数的图象与x轴交于A(﹣3,0)和B(1,0)两点,交y轴于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.
(1)请直接写出D点的坐标.
(2)求二次函数的解析式.
(3)根据图象直接写出使一次函数值大于二次函数值的x的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程k2x2﹣2(k+1)x+1=0有两个实数根.
(1)求k的取值范围;
(2)当k=1时,设所给方程的两个根分别为x1和x2,求(x1﹣2)(x2﹣2)的值.
相关试题

