【题目】某商场在“双十一”促销活动中决定对购买空调的顾客实行现金返利.规定每购买一台空调,商场返利若干元.经调查,销售空调数量y1(单位:台)与返利x(单位:元)之间的函数表达式为![]() .每台空调的利润y2(单位:元)与返利x的函数图像如图所示.
.每台空调的利润y2(单位:元)与返利x的函数图像如图所示.
(1)求y2与x之间的函数表达式;

(2)每台空调返利多少元才能使销售空调的总利润最大?最大总利润是多少?
参考答案:
【答案】(1)![]() ;(2)商场每台空调返利100元时,总利润最大,最大总利润为162000元.
;(2)商场每台空调返利100元时,总利润最大,最大总利润为162000元.
【解析】分析:(1)结合图象信息利用待定系数法求解;
(2)构建二次函数,然后利用配方法确定函数最值问题.
详解:(1)设![]() .
.
根据题意,得![]() .
.
解得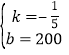 .
.
所以![]() .
.
(2)设该商场销售空调的总利润为w元.
根据题意,得![]() .
.
当x![]() 100时,w的值最大,最大值是162000.
100时,w的值最大,最大值是162000.
所以商场每台空调返利100元时,总利润最大,最大总利润为162000元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】透明的口袋里装有3个球,这3个球分别标有数字1、2、3,这些球除了数字外都相同。
(1)如果从袋中任意摸出一个球,那么摸到标有数字是2的球的概率是多少?(3分)
(2)小明和小东玩摸球游戏,游戏规则如下:先由小明随机摸出一个球,记下球的数字后放回,搅匀后再由小东随机摸出一个球,记下球的数字.谁摸出的球的数字大,谁获胜.现请你利用树状图或列表的方法分析游戏规则对双方是否公平?并说明理由。(6分)
-
科目: 来源: 题型:
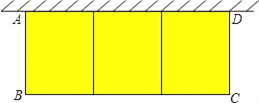
查看答案和解析>>【题目】如图,在一面靠墙的空地上用长为24米的篱笆,围成中间隔有二道篱笆的长方形花圃,设花圃的宽AB为x米,面积为S平方米.
(1)求S与x的函数关系式及自变量的取值范围;
(2)当x取何值时所围成的花圃面积最大,最大值是多少?
(3)若墙的最大可用长度为8米,则求围成花圃的最大面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】两根木条,一根长20cm,另一根长24cm,将它们一端重合且放在同一条直线上,此时两根木条的中点之间的距离为( )
A. 2cm B. 4cm C. 2cm或22cm D. 4cm或44cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】某研究性学习小组在探究矩形的折纸问题时,将一块直角三角板的直角顶点绕矩形ABCD(AB<BC)的对角线的交点O旋转(①→②→③),图中的M、N分别为直角三角形的直角边与矩形ABCD的边CD、BC的交点。
⑴该学习小组成员意外的发现图①(三角板一直角边与OD重合)中,BN2=CD2+CN2,在图③中(三角板一边与OC重合),CN2=BN2+CD2,请你对这名成员在图①和图③中发现的结论选择其一说明理由。

⑵试探究图②中BN、CN、CM、DN这四条线段之间的数量关系,写出你的结论,并说明理由。

⑶将矩形ABCD改为边长为1的正方形ABCD,直角三角板的直角顶点绕O点旋转到图④,两直角边与AB、BC分别交于M、N,直接写出BN、CN、CM、DM这四条线段之 间所满足的数量关系(不需要证明)
-
科目: 来源: 题型:
查看答案和解析>>【题目】一铁棒欲通过一个直角走廊.如图,是该铁棒紧挨着墙角E通过时的两个特殊位置:当铁棒位于AB位置时,它与墙面OG所成的角∠ABO
 51°18′;当铁棒底端B向上滑动1m(即BD
51°18′;当铁棒底端B向上滑动1m(即BD 1m)到达CD位置时,它与墙面OG所成的角∠CDO
1m)到达CD位置时,它与墙面OG所成的角∠CDO 60°,求铁棒的长.(参考数据:sin51°18′
60°,求铁棒的长.(参考数据:sin51°18′ 0.780,cos51°18′
0.780,cos51°18′ 0.625,tan51°18′
0.625,tan51°18′ 1.248)
1.248)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=﹣
 x+2分别交y轴、x轴于A,B两点,抛物线y=﹣x2+bx+c过A,B两点.
x+2分别交y轴、x轴于A,B两点,抛物线y=﹣x2+bx+c过A,B两点.(1)求这个抛物线的解析式;
(2)作垂直于x轴的直线x=t,在第一象限交直线AB于M,交这个抛物线于N.求当t取何值时,△NAB的面积有最大值?最大值是多少?
(3)在(2)的情况下,以A、M、N、D为顶点作平行四边形,求第四个顶点D的坐标.

相关试题

